SONG Shengjie

List: 01背包问题 二维，01背包问题 一维，416. 分割等和子集

01背包问题 二维，01背包问题 一维，416. 分割等和子集partition-equal-subset-sum

01背包问题 二维

Learning Materials

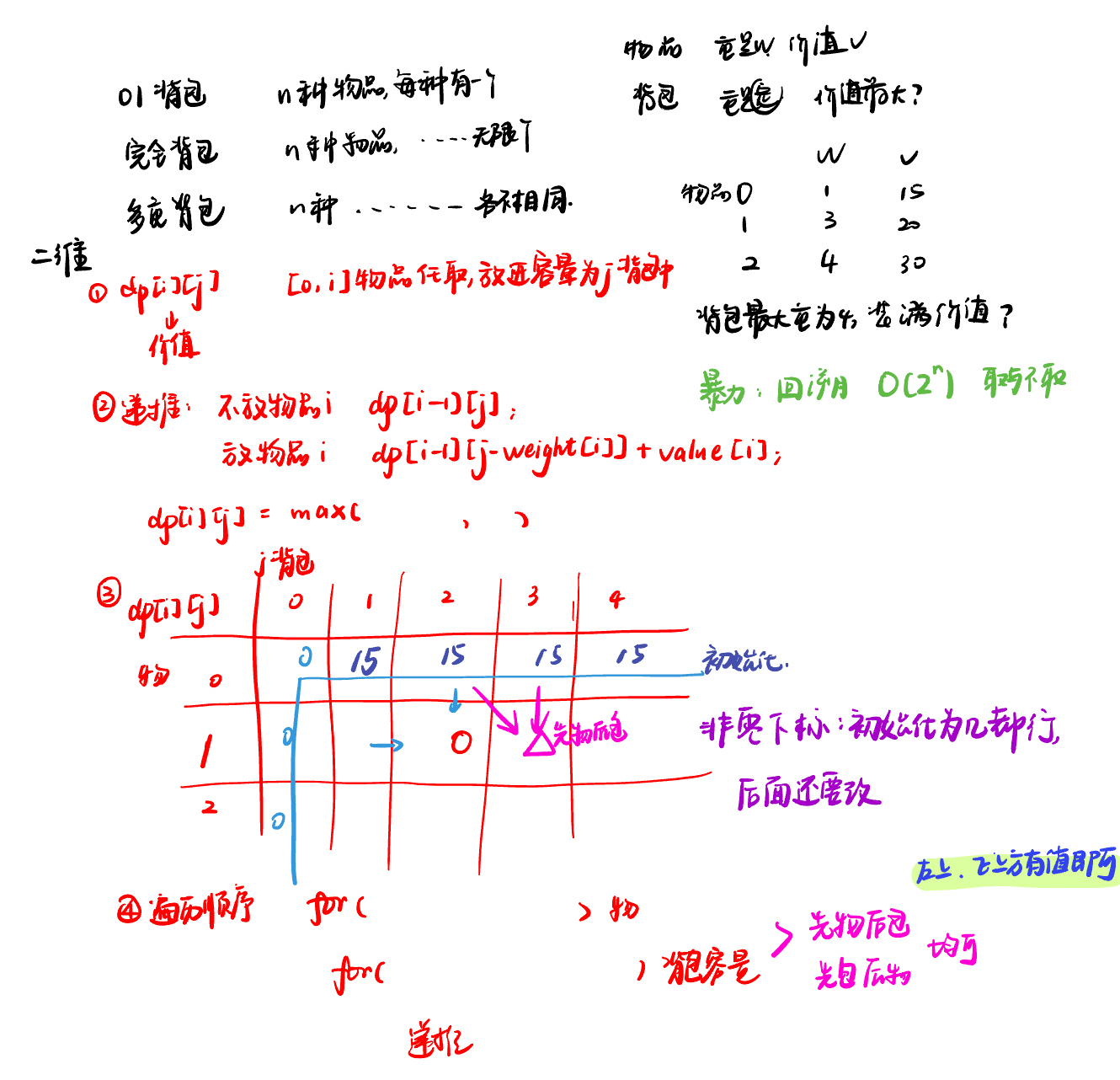
image

n, bagweight = map(int, input().split())

weight = list(map(int, input().split()))
value = list(map(int, input().split()))

dp = [[0] * (bagweight + 1) for _ in range(n)]

for j in range(weight[0], bagweight + 1):
    dp[0][j] = value[0]

for i in range(1, n):
    for j in range(bagweight + 1):
        if j < weight[i]:
            dp[i][j] = dp[i - 1][j]
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

print(dp[n - 1][bagweight])

01背包问题 一维

Learning Materials

image

n, bagweight = map(int, input().split())
weight = list(map(int, input().split()))
value = list(map(int, input().split()))

dp = [0] * (bagweight + 1)  # 创建一个动态规划数组dp，初始值为0

dp[0] = 0  # 初始化dp[0] = 0,背包容量为0，价值最大为0

for i in range(n):  # 应该先遍历物品，如果遍历背包容量放在上一层，那么每个dp[j]就只会放入一个物品
    for j in range(bagweight, weight[i]-1, -1):  # 倒序遍历背包容量是为了保证物品i只被放入一次
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

print(dp[bagweight])

416. 分割等和子集partition-equal-subset-sum

Leetcode

Learning Materials

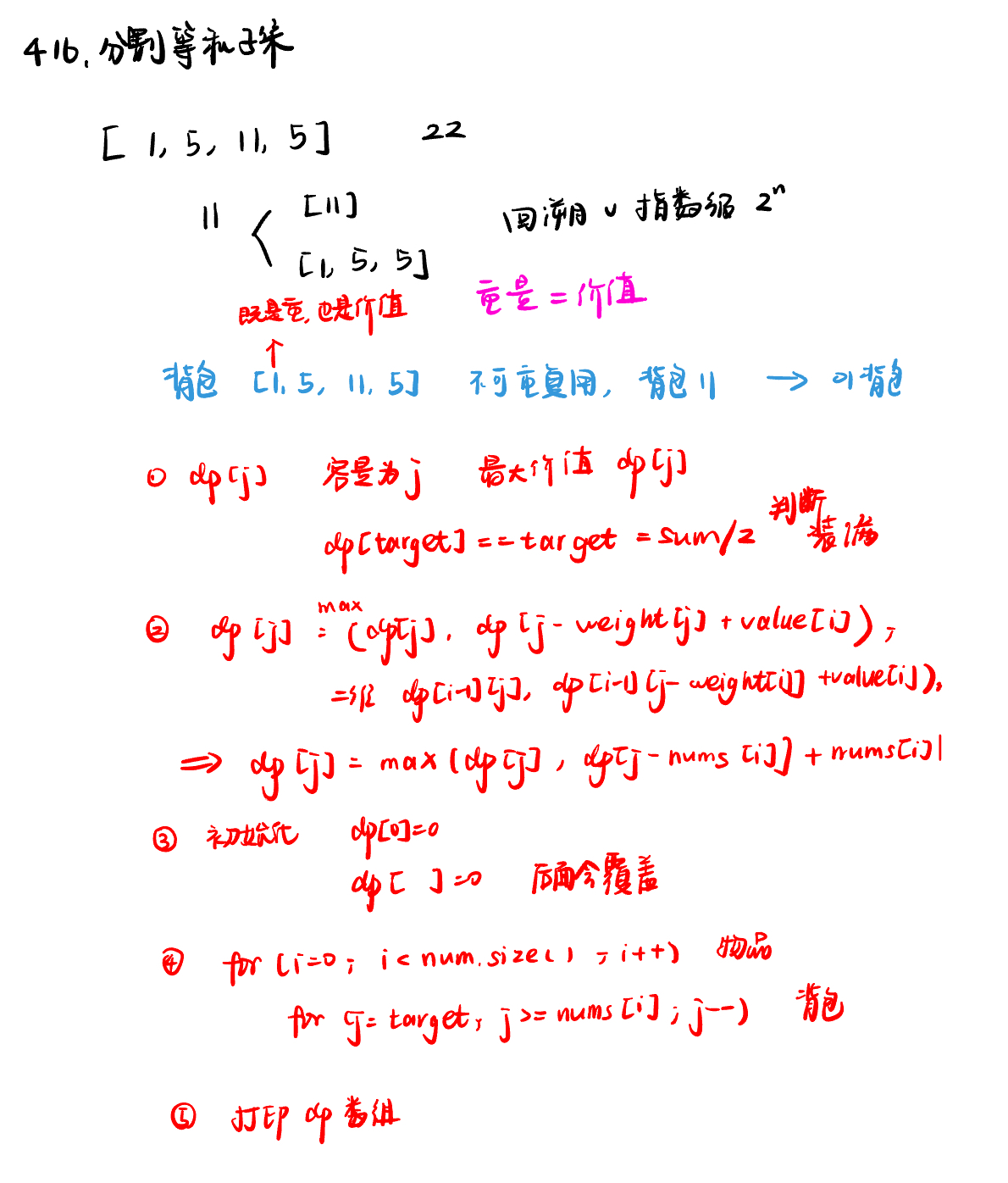
image

一维数组：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        if sum(nums) % 2 != 0:
            return False
        target = sum(nums) // 2
        dp = [0] * (target + 1)
        for i in range(len(nums)):
            for j in range(target, nums[i] - 1, -1):
                dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
        return dp[-1] == target

1. 为什么 dp = [0] * (target + 1) 是 (target + 1)？

在这个问题里，我们的目标是判断给定的数组 nums 是否能够被划分为两个子集，使得这两个子集的元素和相等。若数组元素总和为偶数，那么我们可以把问题转化为：是否能够从数组中选出一些元素，让这些元素的和等于 target = sum(nums) // 2。

这里的 dp 数组是一个一维动态规划数组，dp[j] 表示在考虑数组元素的情况下，能够凑出的不超过 j 的最大和。我们需要计算从 0 到 target 所有可能的和，所以 dp 数组的长度应该是 target + 1，这样就能覆盖从 0 到 target 的所有状态。

例如，若 target = 5，那么我们需要考虑 dp[0]（表示凑出和为 0 的情况）、dp[1]（表示凑出和为 1 的情况）、dp[2]（表示凑出和为 2 的情况）、dp[3]（表示凑出和为 3 的情况）、dp[4]（表示凑出和为 4 的情况）以及 dp[5]（表示凑出和为 5 的情况），总共 6 个状态，因此 dp 数组的长度为 target + 1 = 6。

2. 为什么 for j in range(target, nums[i] - 1, -1) 是 (target, nums[i] - 1)？

这是一个倒序遍历的过程，主要是为了避免重复使用同一个元素。在 0 - 1 背包问题中，每个元素只能使用一次。

二维数组：

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        if sum(nums) % 2 != 0:
            return False
        target = sum(nums) // 2
        
        dp = [[False] * (target + 1) for _ in range(len(nums) + 1)]

        for i in range(len(nums) + 1):
            dp[i][0] = True
        
        for i in range(1, len(nums) + 1):
            for j in range(1, target + 1):
                if j < nums[i - 1]:
                    dp[i][j] = dp[i - 1][j]
                else:
                    dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]
        
        return dp[len(nums)][target]

1. dp = [[False] * (target + 1) for _ in range(len(nums) + 1)] 中行列分别是什么，为什么是 len(nums) + 1 和 target + 1

2. for i in range(len(nums) + 1): dp[i][0] = True 代表什么

这行代码的作用是初始化 dp 数组的第一列。dp[i][0] 表示在前 i 个元素中是否能够选出一些元素，使得它们的和等于 0。显然，无论考虑多少个元素，我们都可以不选任何元素，这样就能凑出和为 0 的情况，所以对于所有的 i（从 0 到 len(nums)），dp[i][0] 都应该为 True。

3. dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]] 为什么用 or，为什么这么推

我们以数组 nums = [1, 5, 11, 5] 为例来详细绘制 dp 数组在状态转移过程中的表格情况。

首先，计算出 target = sum(nums) // 2 = (1 + 5 + 11 + 5) // 2 = 11。

初始化 dp 数组

| i \ j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | | — | — | — | — | — | — | — | — | — | — | — | — | — | | 0 | True | False | False | False | False | False | False | False | False | False | False | False |

这里 i 表示考虑前 i 个元素，j 表示要凑出的目标和。dp[0][0] 初始化为 True，因为不选任何元素时和为 0；其他 dp[0][j]（j > 0）初始化为 False，因为不选元素无法凑出大于 0 的和。

考虑第一个元素 nums[0] = 1（i = 1）

i \ j 0 1 2 3 4 5 6 7 8 9 10 11
0 True False False False False False False False False False False False
1 True True False False False False False False False False False False

考虑第二个元素 nums[1] = 5（i = 2）

i \ j 0 1 2 3 4 5 6 7 8 9 10 11
0 True False False False False False False False False False False False
1 True True False False False False False False False False False False
2 True True False False False True True False False False False False

考虑第三个元素 nums[2] = 11（i = 3）

i \ j 0 1 2 3 4 5 6 7 8 9 10 11
0 True False False False False False False False False False False False
1 True True False False False False False False False False False False
2 True True False False False True True False False False False False
3 True True False False False True True False False False False True

考虑第四个元素 nums[3] = 5（i = 4）

i \ j 0 1 2 3 4 5 6 7 8 9 10 11
0 True False False False False False False False False False False False
1 True True False False False False False False False False False False
2 True True False False False True True False False False False False
3 True True False False False True True False False False False True
4 True True False False False True True False False False True True

最终，我们查看 dp[4][11] 的值为 True，这表明可以将数组 [1, 5, 11, 5] 划分为两个和相等的子集（例如 [1, 5, 5] 和 [11]）。

通过这个表格，我们可以清晰地看到 dp 数组在状态转移过程中是如何根据是否选择当前元素来更新状态的。

This site is open source. Improve this page.