SONG Shengjie
List: 62.不同路径,63. 不同路径 II,343. 整数拆分,96.不同的二叉搜索树
62.不同路径unique-paths,63. 不同路径 IIunique-paths-ii,343. 整数拆分integer-break,96.不同的二叉搜索树unique-binary-search-trees
62.不同路径unique-paths
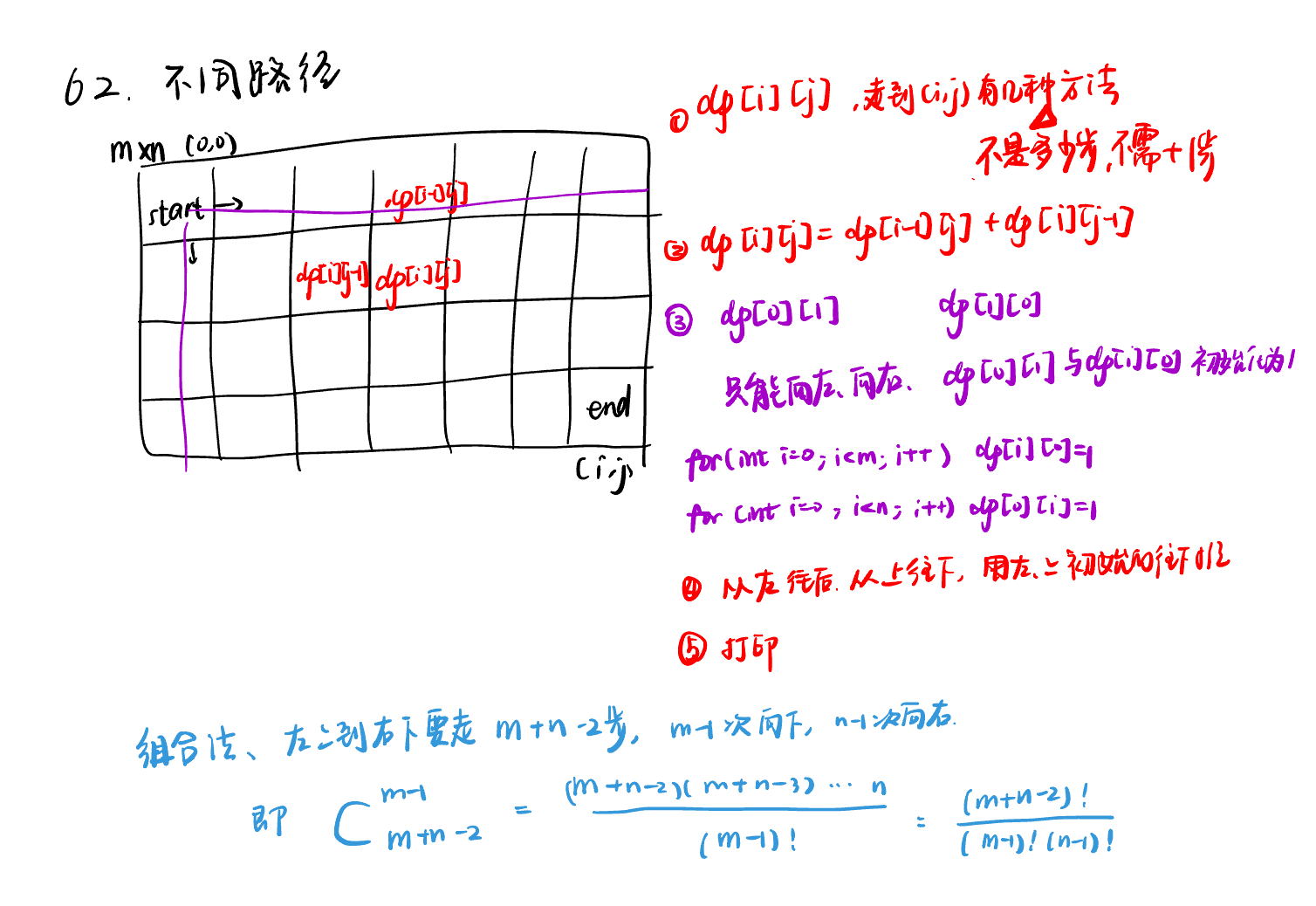
方法一:动态规划
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
if m == 1 or n == 1:
return 1
dp = [[0] * n for _ in range(m)]
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
方法二:滚动数组
由于 f(i,j) 仅与第 i 行和第 i−1 行的状态有关,因此我们可以使用滚动数组代替代码中的二维数组,使空间复杂度降低为 O(n)。
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [1] * n
for i in range(1, m):
for j in range(1, n):
dp[j] += dp[j - 1]
return dp[n - 1]
方法三:组合数
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# 初始化分子为 1,用于存储组合数公式中的分子部分
numerator = 1
# 初始化分母为 m - 1,用于存储组合数公式中的分母部分
denominator = m - 1
# 记录需要进行乘法运算的次数,也就是分子中需要乘的数的个数
count = m - 1
# 计算总共需要移动的步数,即 m + n - 2
t = m + n - 2
# 循环 m - 1 次,计算分子部分
while count > 0:
# 分子乘以当前的步数 t
numerator *= t
# 步数 t 减 1,准备乘下一个数
t -= 1
# 当分母不为 0 且分子能被分母整除时,进行约分操作
while denominator != 0 and numerator % denominator == 0:
# 分子除以分母
numerator //= denominator
# 分母减 1,准备约下一个数
denominator -= 1
# 乘法运算次数减 1
count -= 1
# 最终的分子即为不同路径的数量,返回结果
return numerator
63. 不同路径 IIunique-paths-ii
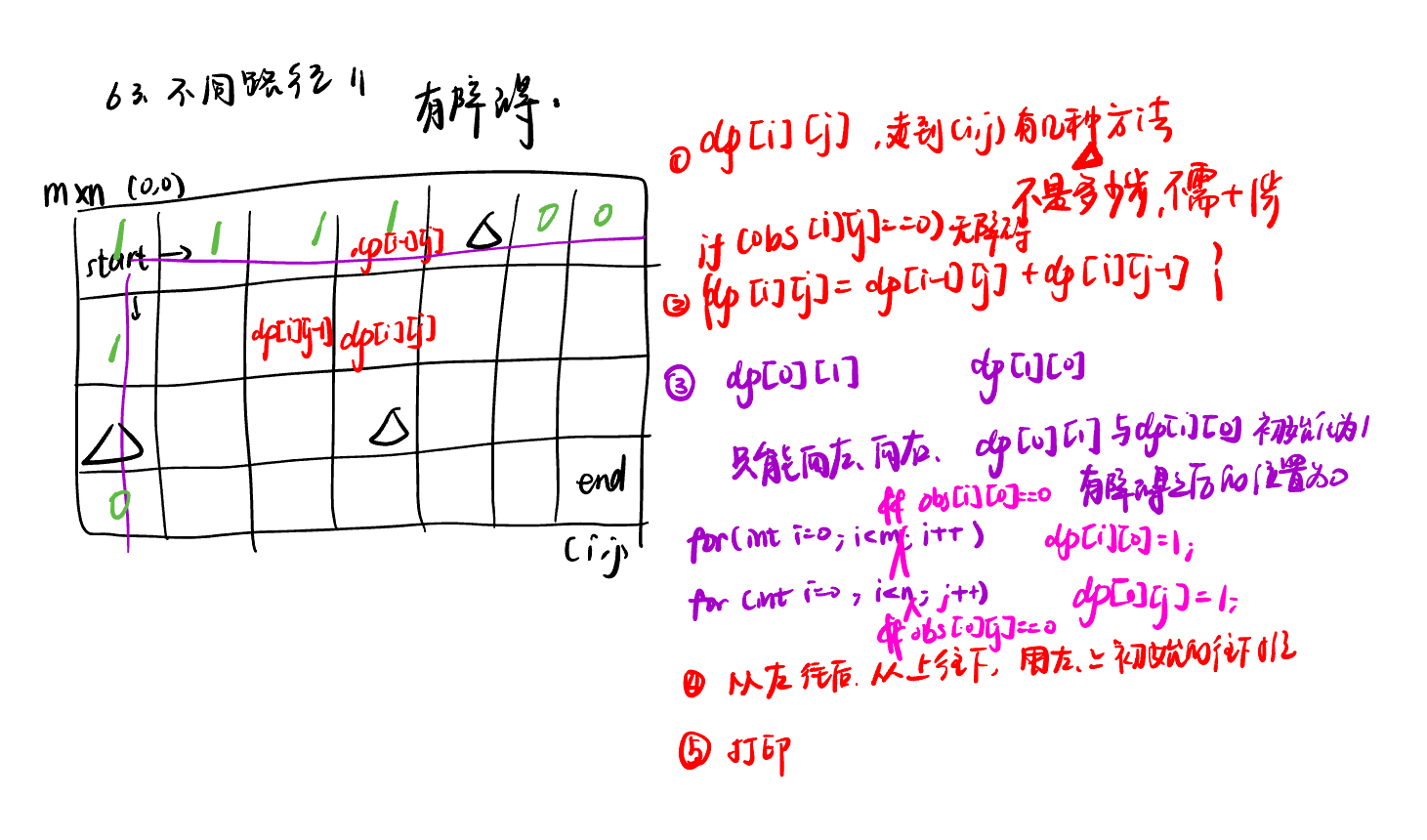
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m = len(obstacleGrid)
n = len(obstacleGrid[0])
if obstacleGrid[0][0] == 1:
return 0
dp = [[0] * n for _ in range(m)]
for i in range(m):
if obstacleGrid[i][0] != 0:
break
dp[i][0] = 1
for j in range(n):
if obstacleGrid[0][j] != 0:
break
dp[0][j] = 1
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 0:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
343. 整数拆分integer-break

class Solution:
def integerBreak(self, n: int) -> int:
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = 0
dp[2] = 1
if n == 2:
return dp[2]
for i in range(3, n + 1):
for j in range(1, i):
dp[i] = max(j * (i - j), j * dp[i - j], dp[i])
return dp[-1]
递推公式的确定
问题背景
我们要把一个正整数 n 拆分成至少两个正整数的和,并且让这些拆分后的正整数的乘积达到最大。为了求解这个问题,我们使用动态规划的方法,创建一个数组 dp,其中 dp[i] 表示把整数 i 拆分成至少两个正整数的和之后,这些正整数所能得到的最大乘积。
1. 两种拆分方式
当我们要计算 dp[i](也就是把整数 i 拆分后得到的最大乘积)时,会从 1 到 i - 1 遍历一个数 j,通过两种不同的拆分方式来尝试得到最大乘积:
- 方式一:
j * (i - j)- 这种方式是把整数
i直接拆分成两个数j和i - j,然后计算它们的乘积。例如,当i = 5,j = 2时,就是把5拆分成2和3,乘积就是2 * 3 = 6。这相当于只把i拆成了两个数相乘的情况。
- 这种方式是把整数
- 方式二:
j * dp[i - j]- 这里的
dp[i - j]表示把i - j这个数拆分成至少两个正整数的和之后得到的最大乘积。所以j * dp[i - j]表示把i拆分成j和对i - j进一步拆分后的结果相乘。例如,当i = 5,j = 2时,i - j = 3,而dp[3]是把3拆分后得到的最大乘积(dp[3] = 2,因为3 = 2 + 1,2 * 1 = 2),那么j * dp[i - j] = 2 * 2 = 4。这相当于把i拆分成两个以上的数相乘的情况。
- 这里的
2. 为什么不拆分 j
在遍历 j 从 1 到 i - 1 的过程中,其实已经考虑过拆分 j 的所有情况了。比如说,当我们计算 dp[5] 时,对于 j = 2,我们考虑了 2 * (5 - 2) 和 2 * dp[5 - 2];当 j = 3 时,又会考虑 3 * (5 - 3) 和 3 * dp[5 - 3]。在这个过程中,就已经涵盖了所有可能的拆分组合,所以不需要再额外拆分 j。
3. 递推公式中的 dp[i]
递推公式 dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j}) 里,要比较 dp[i] 是因为在遍历 j 的过程中,每一次计算 (i - j) * j 和 dp[i - j] * j 都会得到一个新的可能的最大乘积。我们需要不断更新 dp[i],让它始终存储到目前为止所找到的最大乘积。也就是说,在遍历 j 的每一步,都要比较当前得到的乘积和之前已经记录在 dp[i] 中的最大乘积,取其中的最大值作为新的 dp[i]。
示例
假设 i = 4,我们来详细看一下计算 dp[4] 的过程:
- 当
j = 1时:(i - j) * j = (4 - 1) * 1 = 3dp[i - j] * j = dp[3] * 1 = 2 * 1 = 2- 此时
dp[4]初始为0,更新dp[4] = max(0, 3, 2) = 3
- 当
j = 2时:(i - j) * j = (4 - 2) * 2 = 4dp[i - j] * j = dp[2] * 2 = 1 * 2 = 2- 更新
dp[4] = max(3, 4, 2) = 4
- 当
j = 3时:(i - j) * j = (4 - 3) * 3 = 3dp[i - j] * j = dp[1] * 3 = 0 * 3 = 0- 更新
dp[4] = max(4, 3, 0) = 4
最终,dp[4] 的值为 4,这就是把 4 拆分成至少两个正整数的和之后得到的最大乘积(4 = 2 + 2,2 * 2 = 4)。
96.不同的二叉搜索树unique-binary-search-trees

class Solution:
def numTrees(self, n: int) -> int:
dp = [0] * (n + 1)
dp[0] = 1
for i in range(1, n + 1):
for j in range(1, i + 1):
dp[i] += dp[j - 1] * dp[i - j]
return dp[-1]
注意:几乎所有动态规划题目给到的n都是自然数,边界条件注意 + 1.尤其是j循环里面!