SONG Shengjie

List: 647. 回文子串，516.最长回文子序列，动态规划总结

647. 回文子串palindromic-substrings，，

647. 回文子串palindromic-substrings

Leetcode

Learning Materials

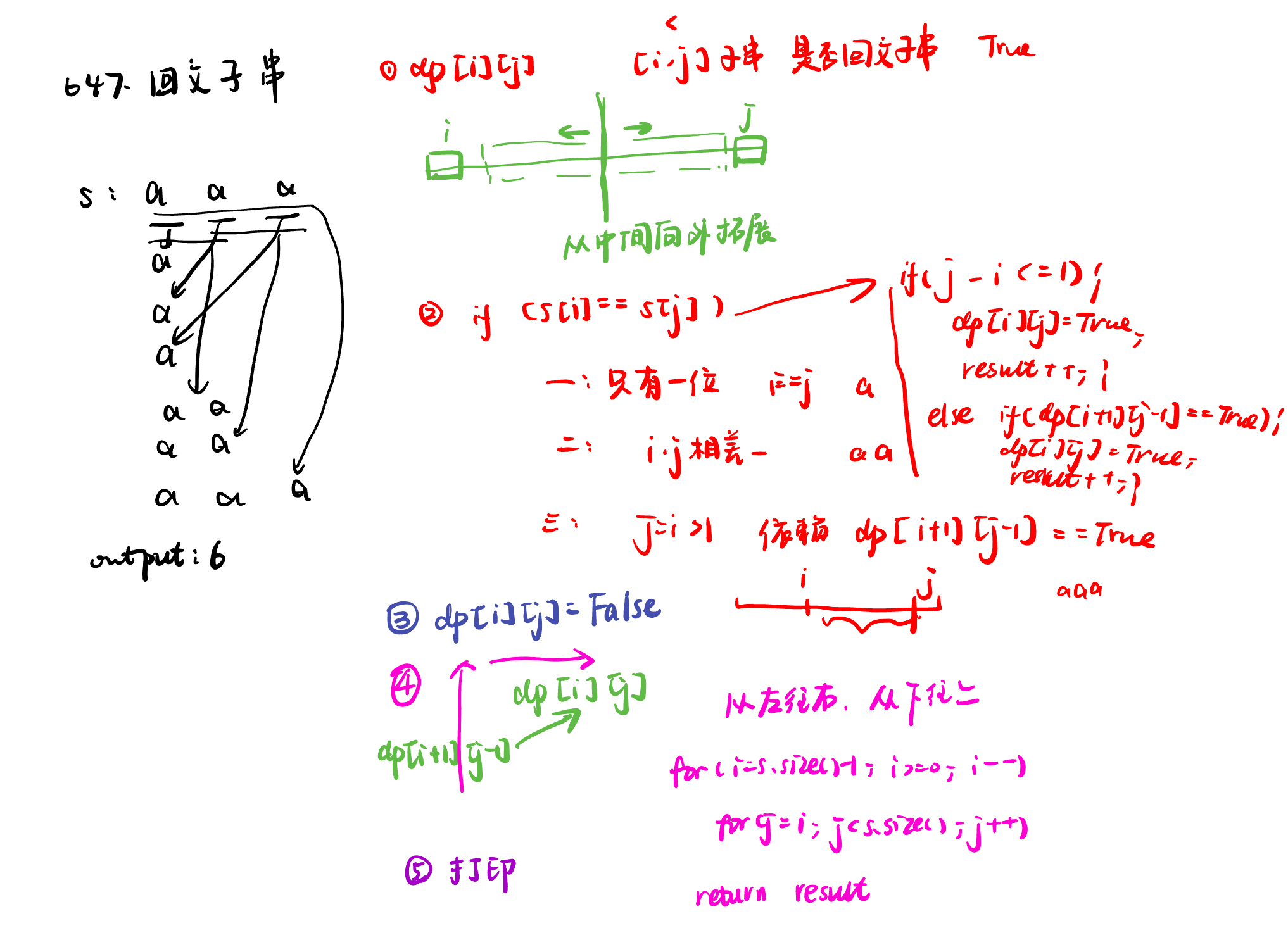
image

class Solution:
    def countSubstrings(self, s: str) -> int:
        dp = [[False] * len(s) for _ in range(len(s))]
        result = 0
        for i in range(len(s) - 1, -1, -1):
            for j in range(i, len(s)):
                if s[i] == s[j]:
                    if j - i <= 1:
                        dp[i][j] = True
                        result += 1
                    elif dp[i + 1][j - 1] == True:
                        dp[i][j] = True
                        result += 1
        return result

双指针法：

class Solution:
    def countSubstrings(self, s: str) -> int:
        result = 0
        for i in range(len(s)):
            result += self.extend(s, i, i, len(s)) #以i为中心
            result += self.extend(s, i, i+1, len(s)) #以i和i+1为中心
        return result
    
    def extend(self, s, i, j, n):
        res = 0
        while i >= 0 and j < n and s[i] == s[j]:
            i -= 1
            j += 1
            res += 1
        return res

516.最长回文子序列longest-palindromic-subsequence

Leetcode

Learning Materials

image

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        dp = [[0] * len(s) for _ in range(len(s))]
        for i in range(len(s)):
            dp[i][i] = 1
        for i in range(len(s) - 1, -1, -1):
            for j in range(i + 1, len(s)):
                if s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
        return dp[0][len(s) - 1]

动态规划总结

Learning Materials

题目名称 题目特点 解题要点 dp数组定义 注意事项
动态规划：斐波那契数 动规入门题 用动规五部曲解题，题目已给出递推公式和dp数组初始化方式 通常dp[i]表示第i个斐波那契数 用于熟悉动规解题方法
动态规划：爬楼梯 类似斐波那契数列 正常应先推导递推公式，再发现其与斐波那契数列的关系；初始化dp[1]=1，dp[2]=2，i从3开始遍历 dp[i]表示爬到第i层楼梯的方法数 dp[0]无意义，可不初始化；可深化为完全背包问题，如一步可爬1到m个台阶的情况
动态规划：使用最小花费爬楼梯 在爬楼梯基础上增加花费 理解题意中体力花费的方式，有不同的dp数组定义方式 可定义为第一步花费体力，最后一步不花费；也可定义为第一步不花费，最后一步花费 两种定义方式都能解题，代码实现略有不同

不同路径（包含无障碍和有障碍两种情况）

整数拆分：对于给定的正整数n，将其拆分为至少两个正整数的和，求这些正整数的最大乘积。定义dp[i]为分拆数字i的最大乘积，只初始化dp[2] = 1 ，因为2只能拆分为1+1，乘积为1。通过双重循环遍历，内层循环从1到i - 1 ，计算dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j)) ，其中(i - j) * j表示将i拆分为j和i - j的乘积，dp[i - j] * j表示将i拆分为i - j和j ，且dp[i - j]是已计算出的最大乘积，取这两者的最大值与当前dp[i]比较并更新。

不同的二叉搜索树：给定一个整数n，求由1到n为节点组成的不同二叉搜索树的个数。定义dp[i]为1到i为节点组成的二叉搜索树的个数 ，初始化只需要dp[0] = 1 ，这是为了后续计算方便，0个节点时可认为有一种空树的情况。通过循环遍历，对于每个i ，内层循环遍历j从1到i ，利用递推公式dp[i] += dp[j - 1] * dp[i - j]计算，其中dp[j - 1]表示以j - 1个节点组成的左子树的数量，dp[i - j]表示以i - j个节点组成的右子树的数量，两者相乘再累加得到dp[i]。

项目 详情
dp[j]定义 填满j（包括j）这么大容积的包，有dp[j]种方法
递推公式 dp[j] += dp[j - nums[i]]
初始化 dp[0]初始化为1，其他下标初始化为0
遍历顺序 nums在外循环，target在内循环且内循环倒序
举例 输入nums: [1, 1, 1, 1, 1]，S: 3，bagSize = 4，展示了dp数组状态变化
项目 详情
dp[i][j]定义 最多有i个0和j个1的strs的最大子集的大小为dp[i][j]
递推公式 dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)，zeroNum和oneNum为字符串中0和1的数量
初始化 初始为0
遍历顺序 外层遍历物品，内层遍历背包容量且从后向前遍历
举例 输入["10","0001","111001","1","0"]，m = 3，n = 3，展示了dp数组最终状态

一、背包问题分类及核心要点

  1. 背包类型： • 0-1背包：物品只能选或不选（每个物品1个）。 • 完全背包：物品可无限次使用。 • 多重背包：物品有数量限制（进阶问题）。 • 特殊变种：分组背包、多维背包等。

  2. 动态规划五步法： • 定义dp数组及下标含义 → 推导递推公式 → 初始化 → 遍历顺序 → 举例验证。

二、递推公式与问题类型对应

问题类型 递推公式 经典例题
能否装满背包（最多装多少） dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]) 分割等和子集、最后一块石头的重量II
装满背包的方法数 dp[j] += dp[j-nums[i]] 零钱兑换II、目标和、组合总和Ⅳ
背包装满后的最大价值 dp[j] = max(dp[j], dp[j-w[i]]+v[i]) 经典0-1背包问题（无具体例题链接）
装满背包的最小物品个数 dp[j] = min(dp[j], dp[j-coins[i]]+1) 零钱兑换、完全平方数

三、遍历顺序核心规律

  1. 0-1背包： • 一维数组实现：必须先遍历物品，背包容量倒序（防重复）。 • 例题：分割等和子集、目标和。

  2. 完全背包： • 求组合数（不考虑顺序）：外层物品，内层背包（正序）。 ◦ 例题：零钱兑换II。 • 求排列数（考虑顺序）：外层背包，内层物品（正序）。 ◦ 例题：组合总和Ⅳ、爬楼梯（进阶版）。 • 求最小值：遍历顺序无影响。 ◦ 例题：零钱兑换、完全平方数。

This site is open source. Improve this page.