SONG Shengjie
List: 1143.最长公共子序列,1035.不相交的线,53. 最大子序和,392.判断子序列
1143.最长公共子序列longest-common-subsequence,1035.不相交的线uncrossed-lines,53. 最大子序和maximum-subarray,392.判断子序列is-subsequence
1143.最长公共子序列longest-common-subsequence
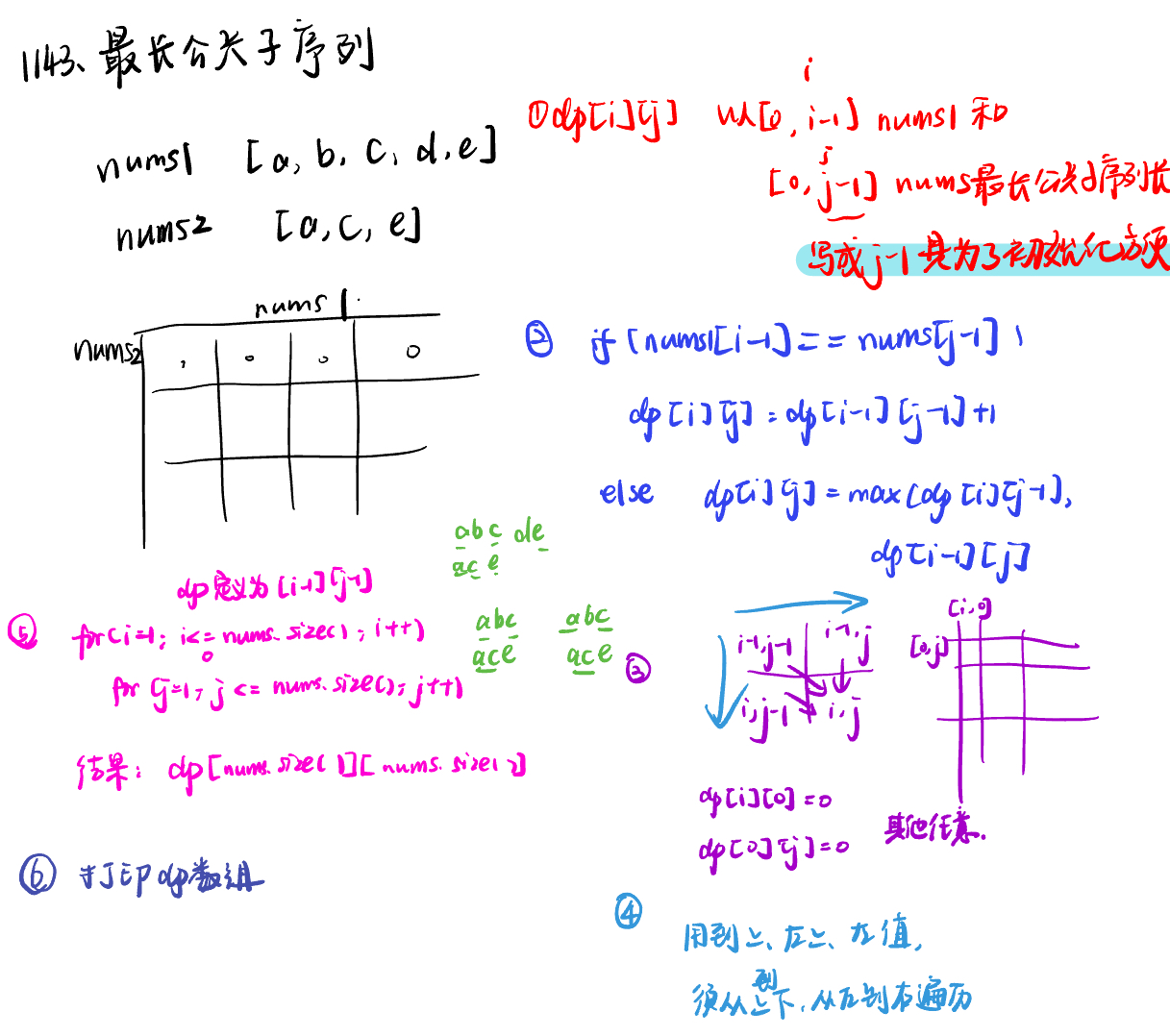
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
for i in range(1, len(text1) + 1):
for j in range(1, len(text2) + 1):
if text1[i - 1] == text2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[len(text1)][len(text2)]
1035.不相交的线uncrossed-lines

- 和上一题完全一样
class Solution:
def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]
for i in range(1, len(nums1) + 1):
for j in range(1, len(nums2) + 1):
if nums1[i - 1] == nums2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[len(nums1)][len(nums2)]
53. 最大子序和maximum-subarray

class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [0] * len(nums)
dp[0] = nums[0]
for i in range(1, len(nums)):
dp[i] = max(dp[i - 1] + nums[i], nums[i])
return max(dp)
392.判断子序列is-subsequence
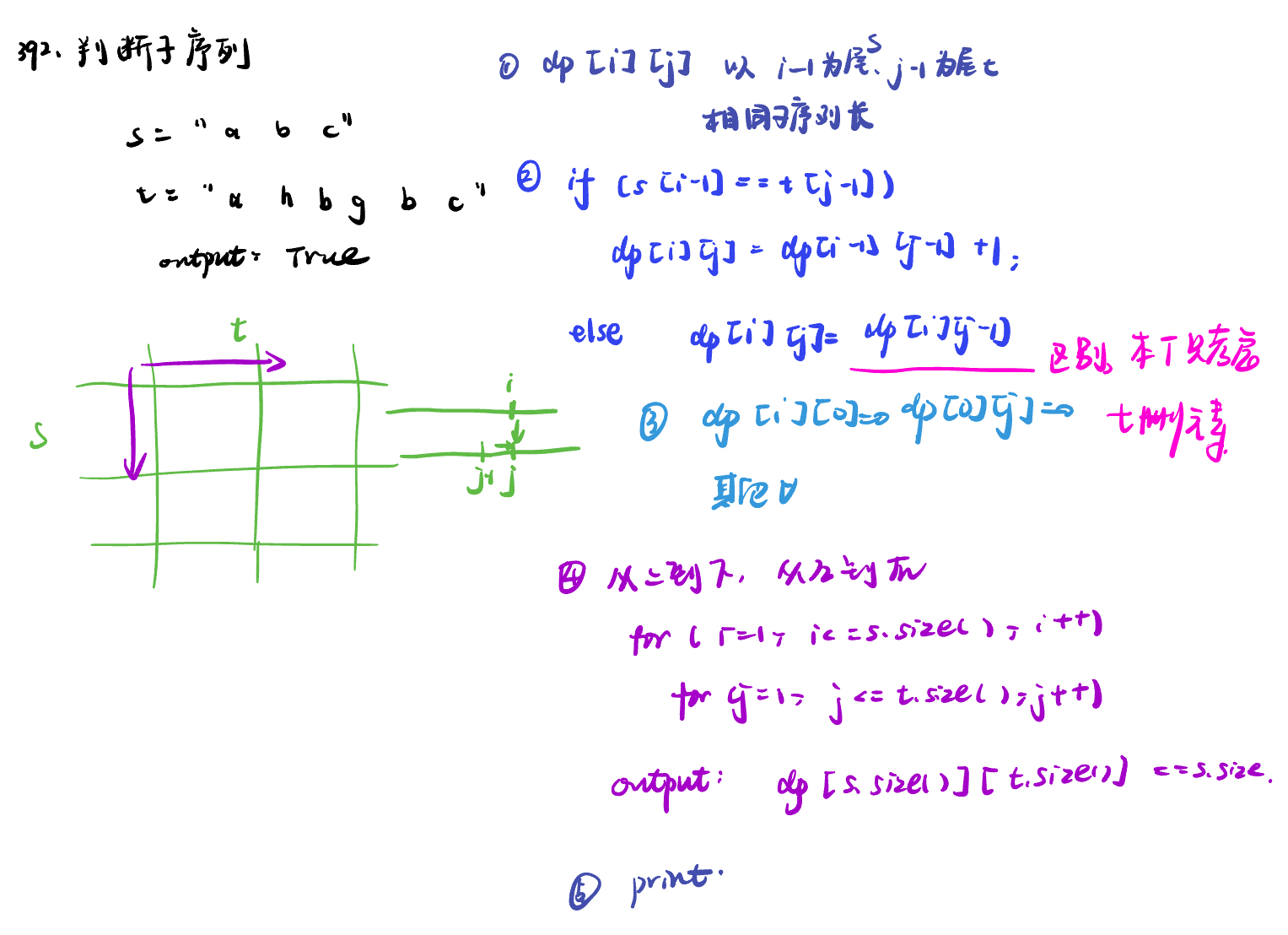
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
dp = [[0] * (len(t) + 1) for _ in range(len(s) + 1)]
for i in range(1, len(s) + 1):
for j in range(1, len(t) + 1):
if s[i - 1] == t[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = dp[i][j - 1]
return dp[len(s)][len(t)] == len(s)