SONG Shengjie
ist: 669. 修剪二叉搜索树,108.将有序数组转换为二叉搜索树,538.把二叉搜索树转换为累加树,538.把二叉搜索树转换为累加树
669. 修剪二叉搜索树trim-a-binary-search-tree,108.将有序数组转换为二叉搜索树convert-sorted-array-to-binary-search-tree,538.把二叉搜索树转换为累加树convert-bst-to-greater-tree,
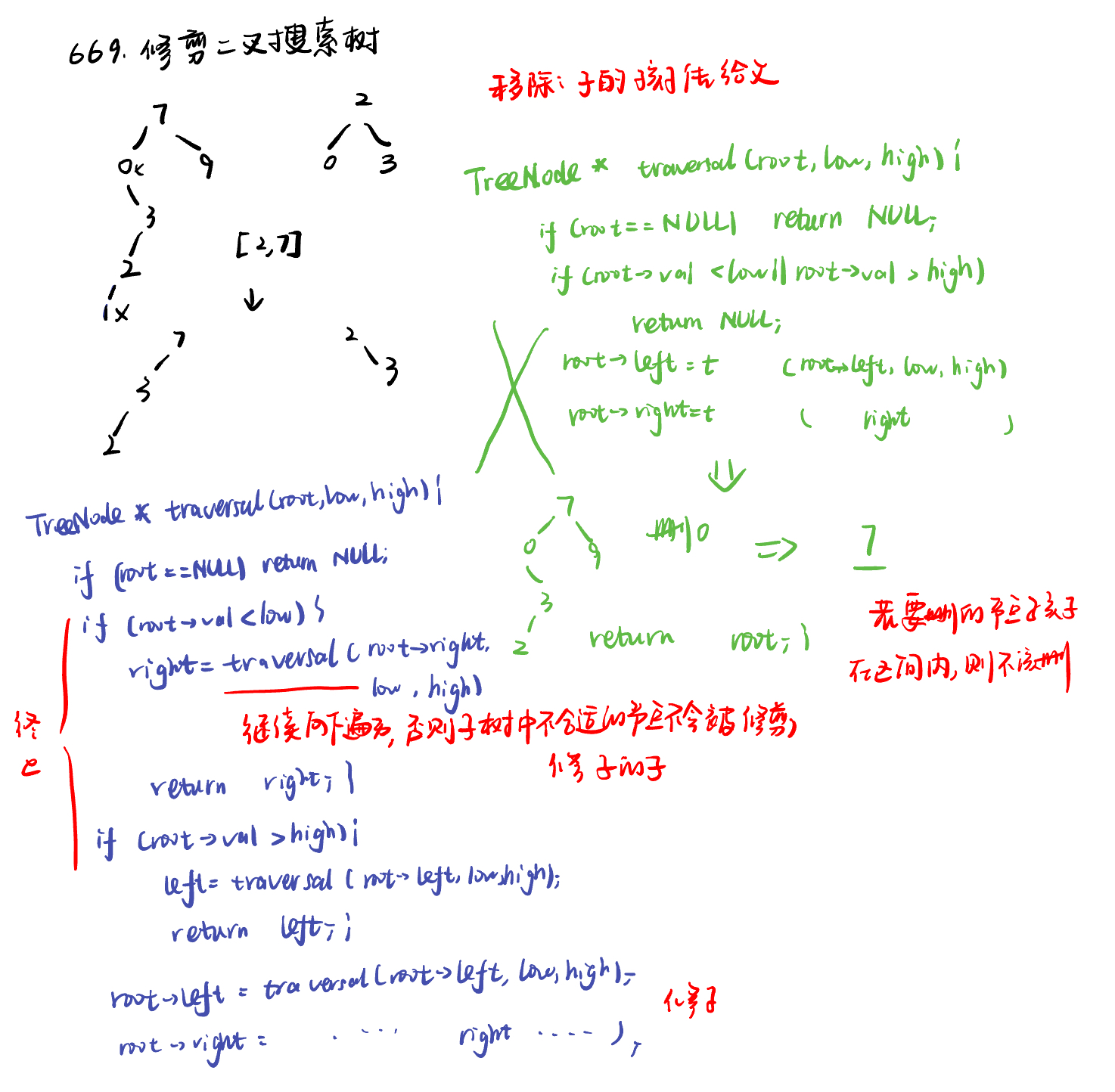
669. 修剪二叉搜索树trim-a-binary-search-tree
class TreeNode:
def __init__(self, val, left = None, right = None):
self.val = val
self.left = left
self.right = right
递归法:
因为二叉搜索树的有序性,不需要使用栈模拟递归的过程。
在剪枝的时候,可以分为三步:
将root移动到[L, R] 范围内,注意是左闭右闭区间
剪枝左子树
剪枝右子树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
if not root:
return
if root.val < low:
right = self.trimBST(root.right, low, high)
return right
if root.val > high:
left = self.trimBST(root.left, low, high)
return left
root.left = self.trimBST(root.left, low, high)
root.right = self.trimBST(root.right, low, high)
return root
迭代法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
if not root:
return
# 处理头结点,让root移动到[L, R] 范围内,注意是左闭右闭
while root and (root.val < low or root.val > high): #不在区间就继续找
if root.val < low:
root = root.right # 二叉搜索有序,小于L往右走
else:
root = root.left # 二叉搜索有序,大于R往左走
cur = root
#此时root已经在[L, R] 范围内,处理左孩子元素小于L的情况
while cur:
while cur.left and cur.left.val < low:
cur.left = cur.left.right #确保把当前节点左子树中所有值小于 low 的节点都修剪掉
cur = cur.left # 检查新的左子树
cur = root # 回退
#此时root已经在[L, R] 范围内,处理右孩子元素大于L的情况
while cur:
while cur.right and cur.right.val > high:
cur.right = cur.right.left
cur = cur.right
return root
108.将有序数组转换为二叉搜索树convert-sorted-array-to-binary-search-tree

递归法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def traversal(self, nums, left, right):
if left > right:
return
mid = (left + right) // 2
root = TreeNode(nums[mid])
root.left = self.traversal(nums, left, mid - 1)
root.right = self.traversal(nums, mid + 1, right)
return root
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
return self.traversal(nums, 0, len(nums) - 1)
迭代法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if len(nums) == 0:
return None
root = TreeNode(0) # 初始根节点
nodeQue = deque() # 放遍历的节点
leftQue = deque() # 保存左区间下标
rightQue = deque() # 保存右区间下标
nodeQue.append(root) # 根节点入队列
leftQue.append(0) # 0为左区间下标初始位置
rightQue.append(len(nums) - 1) # len(nums) - 1为右区间下标初始位置
while nodeQue:
cur = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
mid = left + (right - left) // 2
cur.val = nums[mid] # 把mid传给中间节点
if left <= mid - 1: # 处理左区间
cur.left = TreeNode(0)
nodeQue.append(cur.left)
leftQue.append(left)
rightQue.append(mid - 1)
if right >= mid + 1: # 处理右区间
cur.right = TreeNode(0)
nodeQue.append(cur.right)
leftQue.append(mid + 1)
rightQue.append(right)
return root
538.把二叉搜索树转换为累加树convert-bst-to-greater-tree

递归法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.pre = 0
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return
self.convertBST(root.right)
root.val += self.pre
self.pre = root.val
self.convertBST(root.left)
return root
迭代法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
st = []
cur = root
pre = 0
while cur or st:
if cur:
st.append(cur)
cur = cur.right
else:
cur = st.pop()
cur.val += pre
pre = cur.val
cur = cur.left
return root
理论基础
涉及到二叉树的构造,无论普通二叉树还是二叉搜索树一定前序,都是先构造中节点。
求普通二叉树的属性,一般是后序,一般要通过递归函数的返回值做计算。
求二叉搜索树的属性,一定是中序了,要不白瞎了有序性了。