SONG Shengjie
List: 654.最大二叉树,617.合并二叉树,700.二叉搜索树中的搜索,98.验证二叉搜索树
654.最大二叉树maximum-binary-tree,617.合并二叉树merge-two-binary-trees,700.二叉搜索树中的搜索search-in-a-binary-search-tree,98.验证二叉搜索树validate-binary-search-tree
654.最大二叉树maximum-binary-tree

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
if len(nums) == 1:
return TreeNode(nums[0])
maxvalue, index = 0, 0
for i in range(len(nums)):
if maxvalue < nums[i]:
maxvalue = nums[i]
index = i
node = TreeNode(maxvalue)
if index > 0:
lnums = nums[:index]
node.left = self.constructMaximumBinaryTree(lnums)
if index < len(nums) - 1:
rnums = nums[index + 1:]
node.right = self.constructMaximumBinaryTree(rnums)
return node
优化:不使用新数组,直接用下标:
允许空节点进入递归,所以不用在递归的时候加判断节点是否为空。终止条件也要有相应的改变。
类似用数组构造二叉树的题目,每次分隔尽量不要定义新的数组,而是通过下标索引直接在原数组上操作,这样可以节约时间和空间上的开销。
要不要加if?如果让空节点(空指针)进入递归,就不加if,如果不让空节点进入递归,就加if限制一下, 终止条件也会相应的调整。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
return self.construct(nums, 0, len(nums))
def construct(self, nums, left, right):
#在左闭右开区间[left, right),构造二叉树
if left >= right: #左闭右开区间,相等时为空
return
# 分割点下标:
index = left
for i in range(left, right): #只需要在 [left, right) 这个区间内找到最大值
if nums[index] < nums[i]:
index = i
node = TreeNode(nums[index])
# 左闭右开:[left, maxValueIndex)
node.left = self.construct(nums, left, index)
# 左闭右开:[maxValueIndex + 1, right)
node.right = self.construct(nums, index + 1, right)
return node
617.合并二叉树merge-two-binary-trees

递归法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if not root1:
return root2
if not root2:
return root1
root1.val += root2.val
root1.left = self.mergeTrees(root1.left, root2.left)
root1.right = self.mergeTrees(root1.right, root2.right)
return root1
- 递归的下面顺序也是可以的
root1.left = self.mergeTrees(root1.left, root2.left)
root1.val += root2.val
root1.right = self.mergeTrees(root1.right, root2.right)
root1.left = self.mergeTrees(root1.left, root2.left)
root1.right = self.mergeTrees(root1.right, root2.right)
root1.val += root2.val
迭代法:
使用队列、层序遍历。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
if not root1:
return root2
if not root2:
return root1
que = deque()
que.append(root1)
que.append(root2)
#用队列处理两个要相加的情况,直接在t1上修改,只需要额外考虑t1空而t2不空的情况。
while que:
node1 = que.popleft()
node2 = que.popleft()
#此时两个节点一定不为空,val相加
node1.val += node2.val
#如果两棵树左节点都不为空,加入队列
if node1.left and node2.left:
que.append(node1.left)
que.append(node2.left)
#如果两棵树右节点都不为空,加入队列
if node1.right and node2.right:
que.append(node1.right)
que.append(node2.right)
#当t1的左节点 为空 t2左节点不为空,就赋值过去
if not node1.left and node2.left:
node1.left = node2.left
#当t1的右节点 为空 t2右节点不为空,就赋值过去
if not node1.right and node2.right:
node1.right = node2.right
return root1
700.二叉搜索树中的搜索search-in-a-binary-search-tree
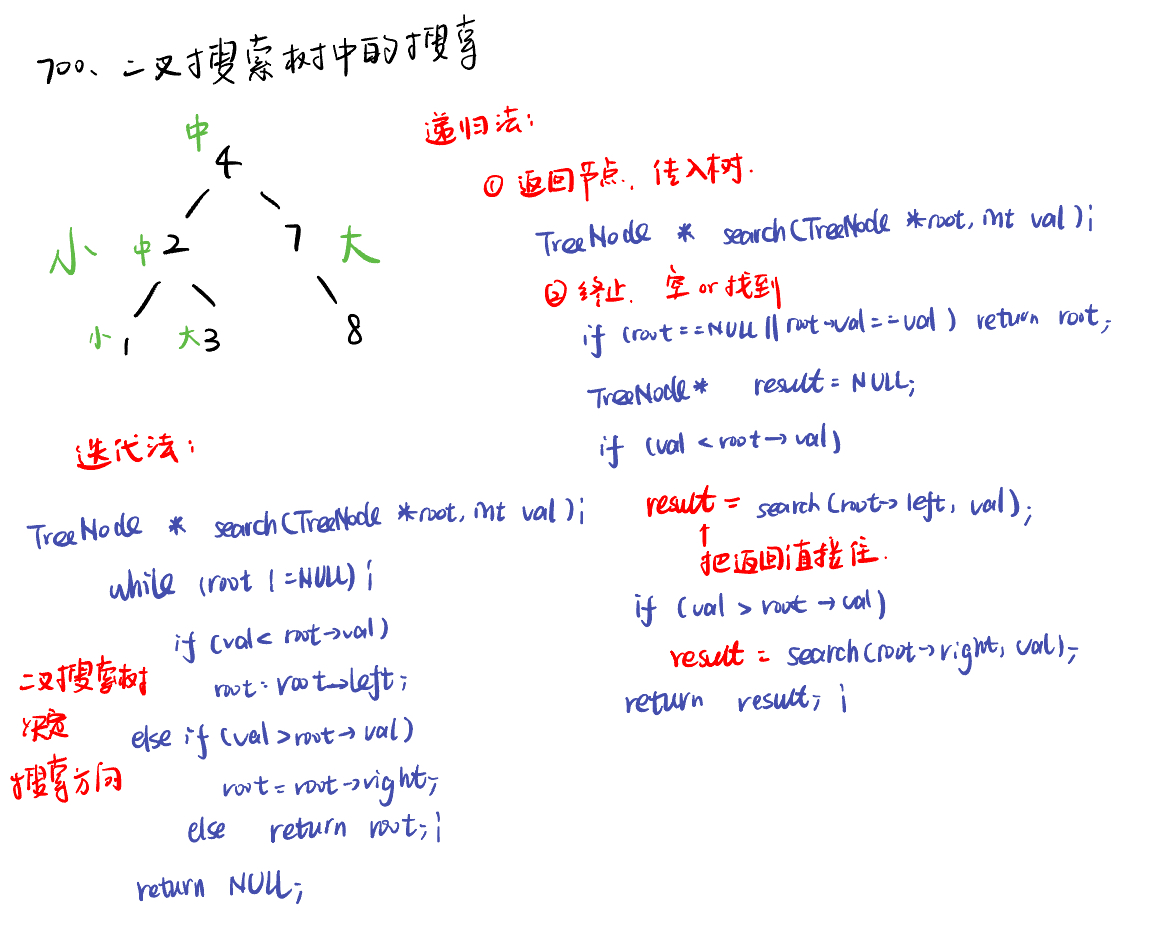
递归法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
if not root or root.val == val:
return root
if root.val > val:
result = self.searchBST(root.left, val)
if root.val < val:
result = self.searchBST(root.right, val)
return result
迭代法:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
while root:
if root.val > val:
root = root.left
elif root.val < val:
root = root.right
else:
return root
return None
98.验证二叉搜索树validate-binary-search-tree

方法一:中序+检查顺序
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
self.result = []
self.isValid(root)
for i in range(1, len(self.result)):
if self.result[i - 1] >= self.result[i]: #注意要小于等于,搜索树里不能有相同元素
return False
return True
def isValid(self, root):
if not root:
return True
self.isValid(root.left)
self.result.append(root.val)
self.isValid(root.right)
方法二:不额外用数组判定顺序,直接在递归中判断
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
self.value = float('-inf')
return self.isValid(root)
def isValid(self, root):
if not root:
return True
left = self.isValid(root.left)
if root.val > self.value:
self.value = root.val
else:
return False
right = self.isValid(root.right)
return left and right
方法三:由于测试数据中有很小的数,用双指针判断,记录前一个节点:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
self.pre = None
return self.isValid(root)
def isValid(self, root):
if not root:
return True
left = self.isValid(root.left)
if self.pre and root.val <= self.pre.val:
return False
self.pre = root
right = self.isValid(root.right)
return left and right
方法四:迭代法,直接在中序遍历上改编
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
st = []
node = root
pre = None
while st and node:
if node:
st.append(node)
node = node.left #左
else:
node = node.pop() #弹出的数据就是要处理的数据, 中
if pre and node.val <= pre.val:
return False
pre = node # 保存前一个节点的值
node = node.right #右
return True
```