SONG Shengjie
List: 226.翻转二叉树,101. 对称二叉树(含100.相同的树、572.另一个树的子树),104.二叉树的最大深度(含559.n叉树的最大深度),111.二叉树的最小深度
226.翻转二叉树invert-binary-tree,101. 对称二叉树symmetric-tree,104.二叉树的最大深度maximum-depth-of-binary-tree,111.二叉树的最小深度minimum-depth-of-binary-tree
后序遍历的本质是把子节点信息记录传给父节点!
226.翻转二叉树invert-binary-tree
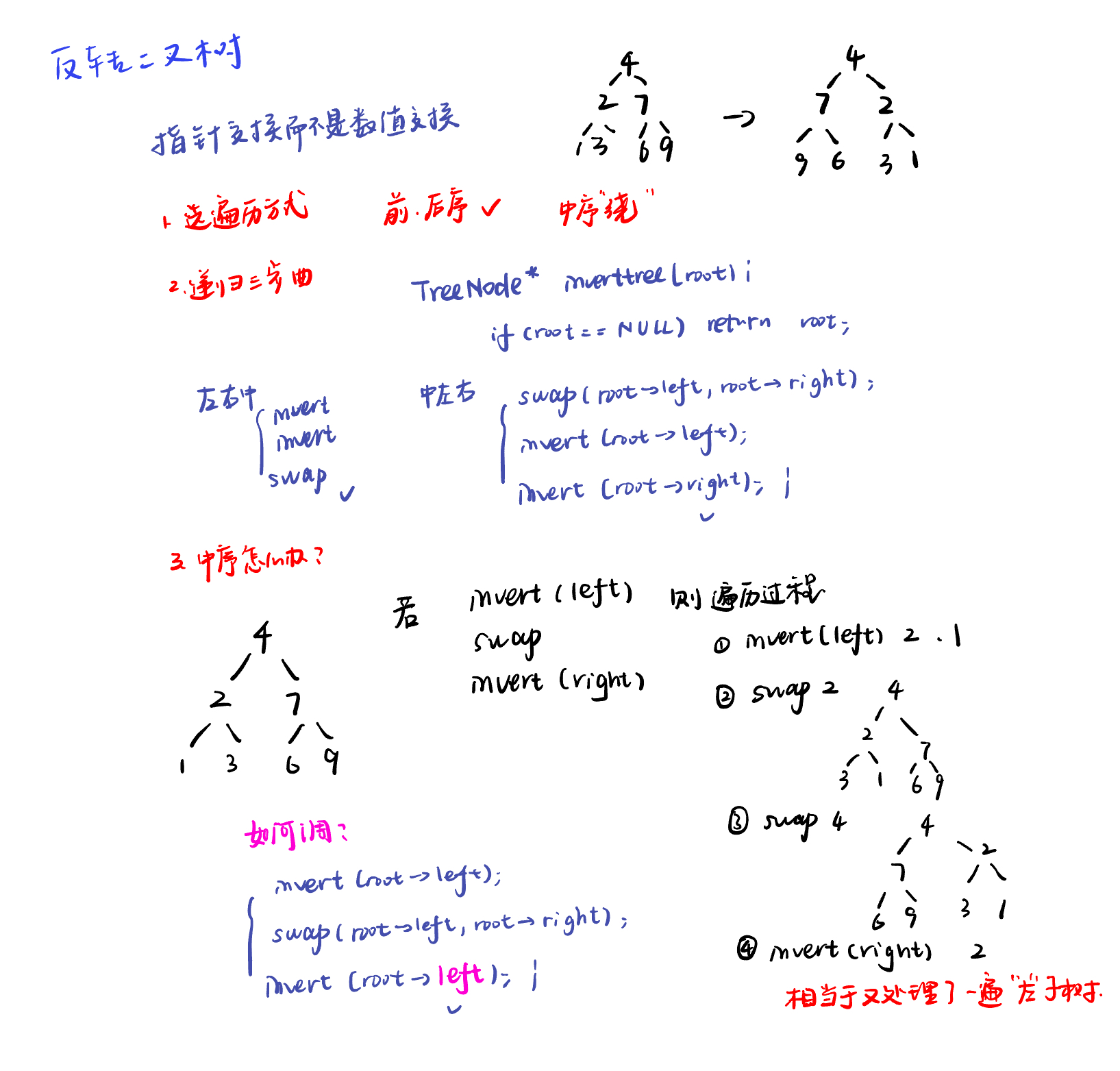
前序遍历:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
后序遍历:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
self.invertTree(root.left)
self.invertTree(root.right)
root.left, root.right = root.right, root.left
return root
中序遍历:递归
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return None
self.invertTree(root.left)
root.left, root.right = root.right, root.left
self.invertTree(root.left)
return root
前序遍历:迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return
st = [root]
while st:
node = st.pop()
node.left, node.right = node.right, node.left
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
return root
伪后序遍历:迭代(实际上它是前序遍历,只不过把中间节点处理逻辑放到了最后)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return
st = [root]
while st:
node = st.pop()
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
node.left, node.right = node.right, node.left
return root
伪中序遍历:迭代(实际上它是前序遍历,只不过把中间节点处理逻辑放到了中间。)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return
st = [root]
while st:
node = st.pop()
if node.right:
st.append(node.right)
node.left, node.right = node.right, node.left
if node.right:
st.append(node.right)
return root
层序遍历:迭代
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
if not root:
return
que = deque([root])
while que:
node = que.popleft()
node.left, node.right = node.right, node.left
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
return root
101. 对称二叉树symmetric-tree
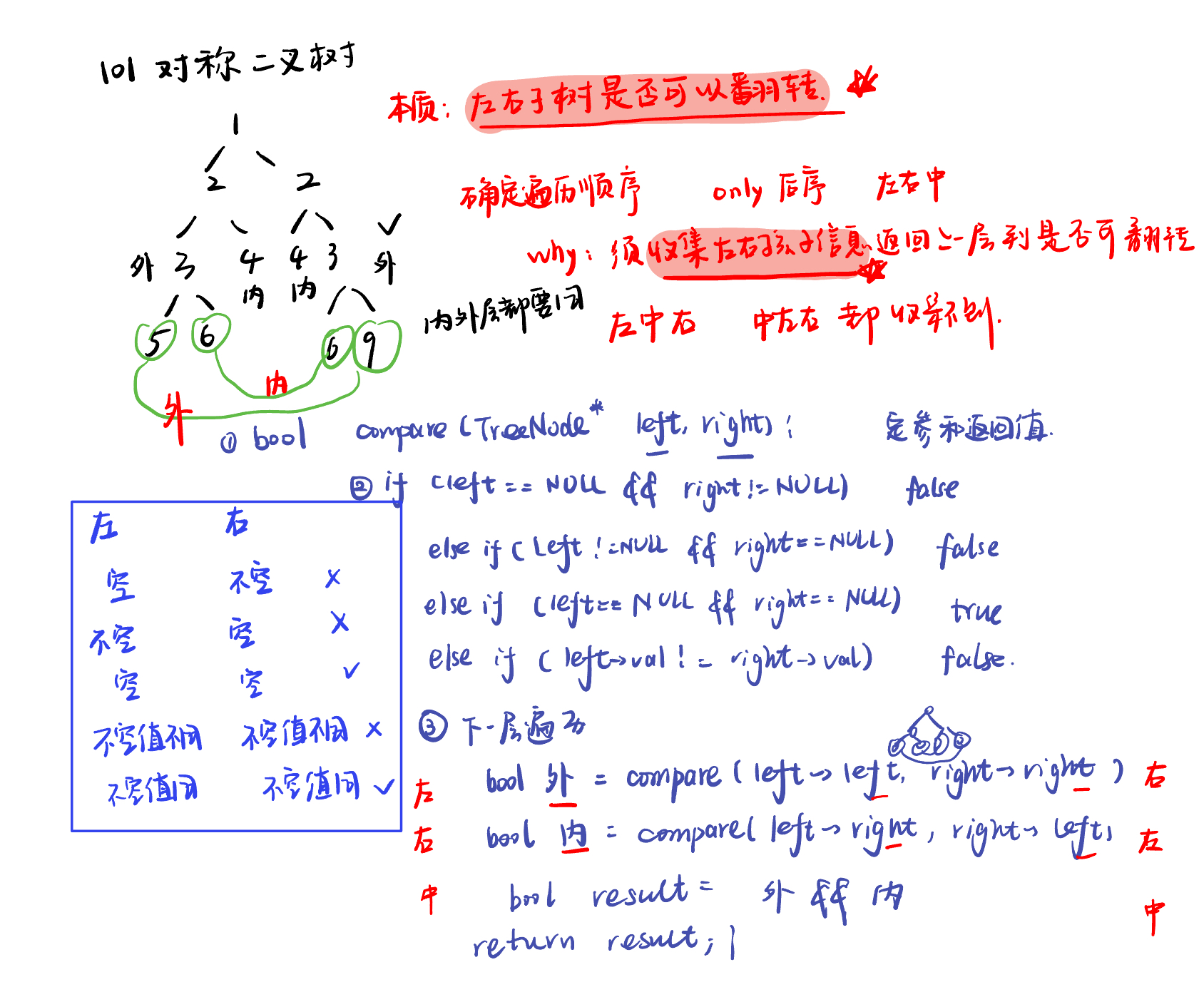
递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
def comparenode(left, right):
if not left and right:
return False
if left and not right:
return False
if not left and not right:
return True
if left.val != right.val:
return False
outside = comparenode(left.left, right.right)
inside = comparenode(left.right, right.left)
return inside and outside
return comparenode(root.left, root.right)
迭代法:
本题并非用二叉树前中后序的迭代法求解,毕竟其核心是判断两棵树(根节点的左右子树)是否相互翻转,与二叉树遍历的前中后序关系不大。
我们可以借助队列来判断这两棵树是否相互翻转(注意,这并非层序遍历)。
使用队列
思路就是两两进队列,两两判断。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
que = deque()
que.append(root.left)
que.append(root.right)
while que:
left = que.popleft()
right = que.popleft()
if not left and right:
return False
if left and not right:
return False
if not left and not right:
continue
if left.val != right.val:
return False
que.append(left.left)
que.append(right.right)
que.append(left.right)
que.append(right.left)
return True
使用栈
思路还是两两进,两两判断,上述方法的本质都是把左右两个子树要比较的元素顺序放进一个容器,然后成对成对的取出来进行比较。
由于两两进,两两出,这“两两”的顺序无所谓,所以无所谓栈和队列。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
st = []
st.append(root.left)
st.append(root.right)
while st:
left = st.pop()
right = st.pop()
if not left and right:
return False
if left and not right:
return False
if not left and not right:
continue
if left.val != right.val:
return False
st.append(left.left)
st.append(right.right)
st.append(left.right)
st.append(right.left)
return True
变式训练、相关题目
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if (p and not q) or (not p and q):
return False
elif (not p and not q):
return True
root = TreeNode(0, left = p, right = q)
def comparenode(left, right):
if not left and right:
return False
if left and not right:
return False
if not left and not right:
return True
if left.val != right.val:
return False
outside = comparenode(left.left, right.left)
inside = comparenode(left.right, right.right)
return inside and outside
return comparenode(root.left, root.right)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not root:
return False
if self.comparenode(root, subRoot):
return True
return self.isSubtree(root.left, subRoot) or self.isSubtree(root.right, subRoot)
def comparenode(self, p, q):
if not p and q:
return False
if p and not q:
return False
if not p and not q:
return True
if p.val != q.val:
return False
return self.comparenode(p.left, q.left) and self.comparenode(p.right, q.right)
104.二叉树的最大深度maximum-depth-of-binary-tree
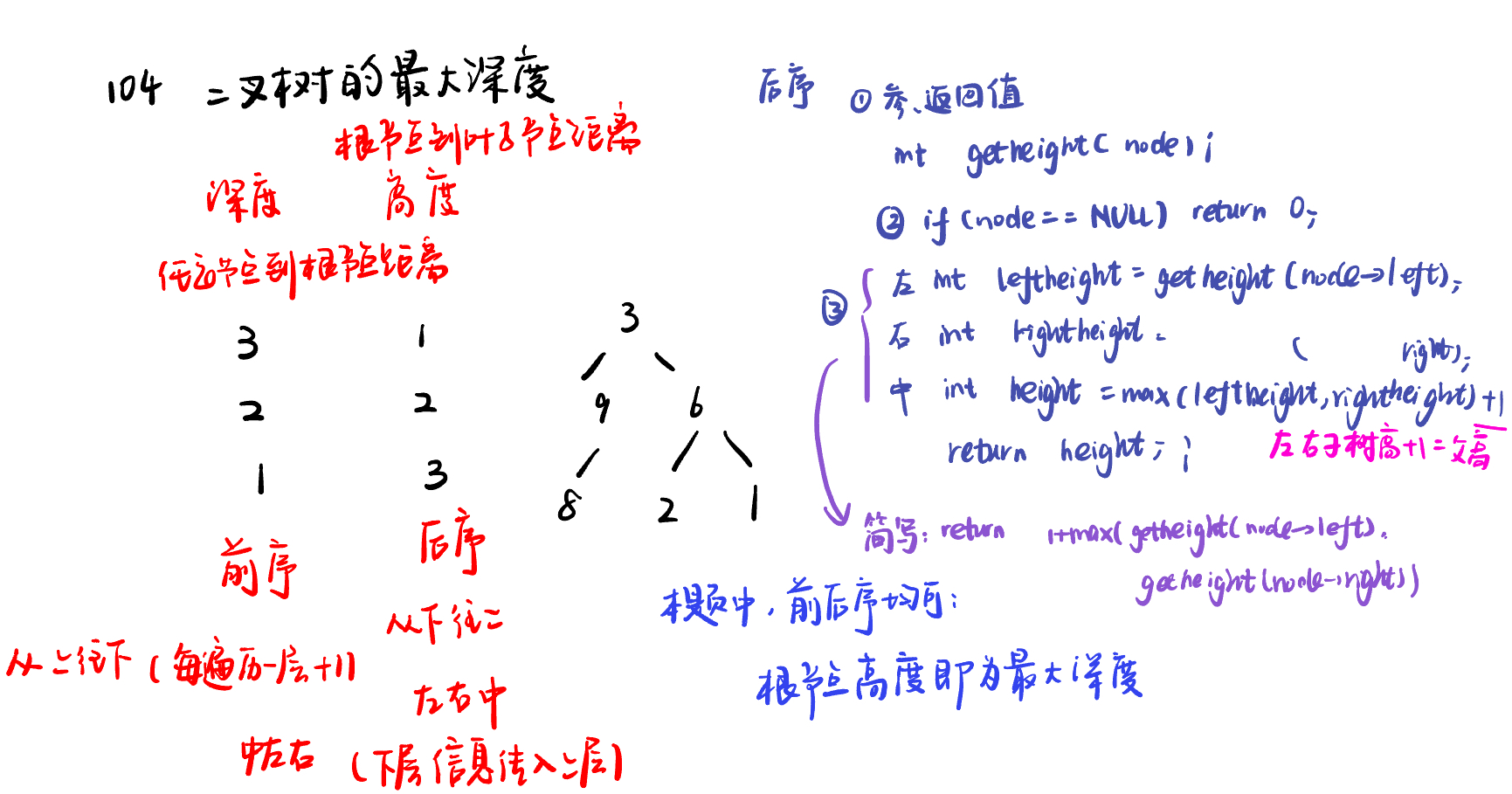
递归-后序遍历求高度:根节点的最大高度就是本题要求的二叉树的最大深度
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
leftheight = self.maxDepth(root.left)
rightheight = self.maxDepth(root.right)
height = 1 + max(leftheight, rightheight)
return height
- 极简版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root: return 0
return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))
递归:前序遍历求高度——回溯的思想
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
self.res = 0
self.getdepth(root, 1)
return self.res
def getdepth(self, node, depth):
self.res = max(self.res, depth)
if not node.left and not node.right:
return
if node.left:
self.getdepth(node.left, depth + 1) #深度先+1,再回溯。全部代码应该是:depth += 1;self.getdepth(node.left, depth); depth -= 1
if node.right:
self.getdepth(node.right, depth + 1)
return
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法。
在计算二叉树最大深度的代码中,回溯思想主要体现在递归调用的过程中。当我们递归地探索二叉树的每个节点时,每次进入一个新的节点,深度就加 1,相当于向前探索;当探索完一个节点及其子树后,递归调用返回,回到上一层节点,这就相当于回溯。
迭代-层序遍历:
最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
只需要加入一个变量来记录深度即可。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
que = deque([root])
depth = 0
while que:
size = len(que)
depth += 1
for i in range(size):
node = que.popleft()
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
return depth
相关题目:
"""
# Definition for a Node.
class Node:
def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
self.val = val
self.children = children
"""
class Solution:
def maxDepth(self, root: 'Node') -> int:
if not root:
return 0
depth = 0
for i in range(len(root.children)):
depth = max(depth, self.maxDepth(root.children[i]))
return depth + 1
111.二叉树的最小深度minimum-depth-of-binary-tree
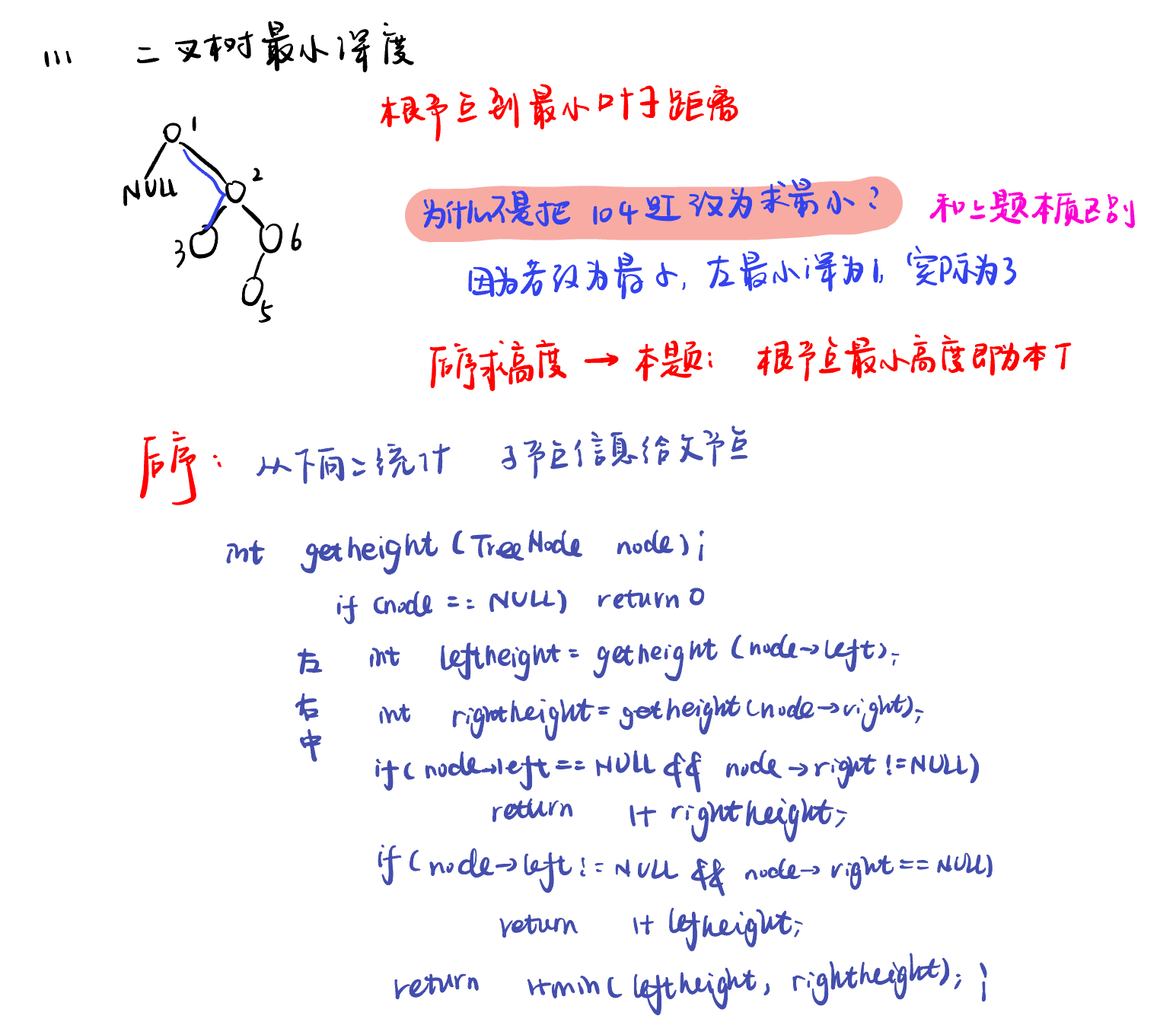
后序遍历:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
leftheight = self.minDepth(root.left)
rightheight = self.minDepth(root.right)
if not root.left and root.right:
return 1 + rightheight
if root.left and not root.right:
return 1 + leftheight
return 1 + min(leftheight, rightheight)
- 精简版:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
if not root.left and root.right:
return 1 + self.minDepth(root.right)
if root.left and not root.right:
return 1 + self.minDepth(root.left)
return 1 + min(self.minDepth(root.left), self.minDepth(root.right))
- 层次遍历:当左右孩子都为空的时候,说明是最低点的一层了,退出。代码见上一节层次遍历的例题。
前序遍历:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
if not root:
return 0
self.res = float('inf')
self.getdepth(root, 1)
return self.res
#self.属性名 时,定义的是实例属性,该属性会绑定到类的具体实例上。而直接使用 变量名 定义的是局部变量,它只在当前函数的作用域内有效。
def getdepth(self, node, depth):
if not node:
return 0
if not node.left and not node.right:
self.res = min(self.res, depth)
if node.left:
self.getdepth(node.left, depth + 1)
if node.right:
self.getdepth(node.right, depth + 1)