SONG Shengjie

List: 理论基础，二叉树的递归遍历，二叉树的迭代遍历，二叉树的统一迭代法，二叉树的层序遍历

理论基础，二叉树的递归遍历，二叉树的迭代遍历，二叉树的统一迭代法,二叉树的层序遍历

理论基础

Learning Materials

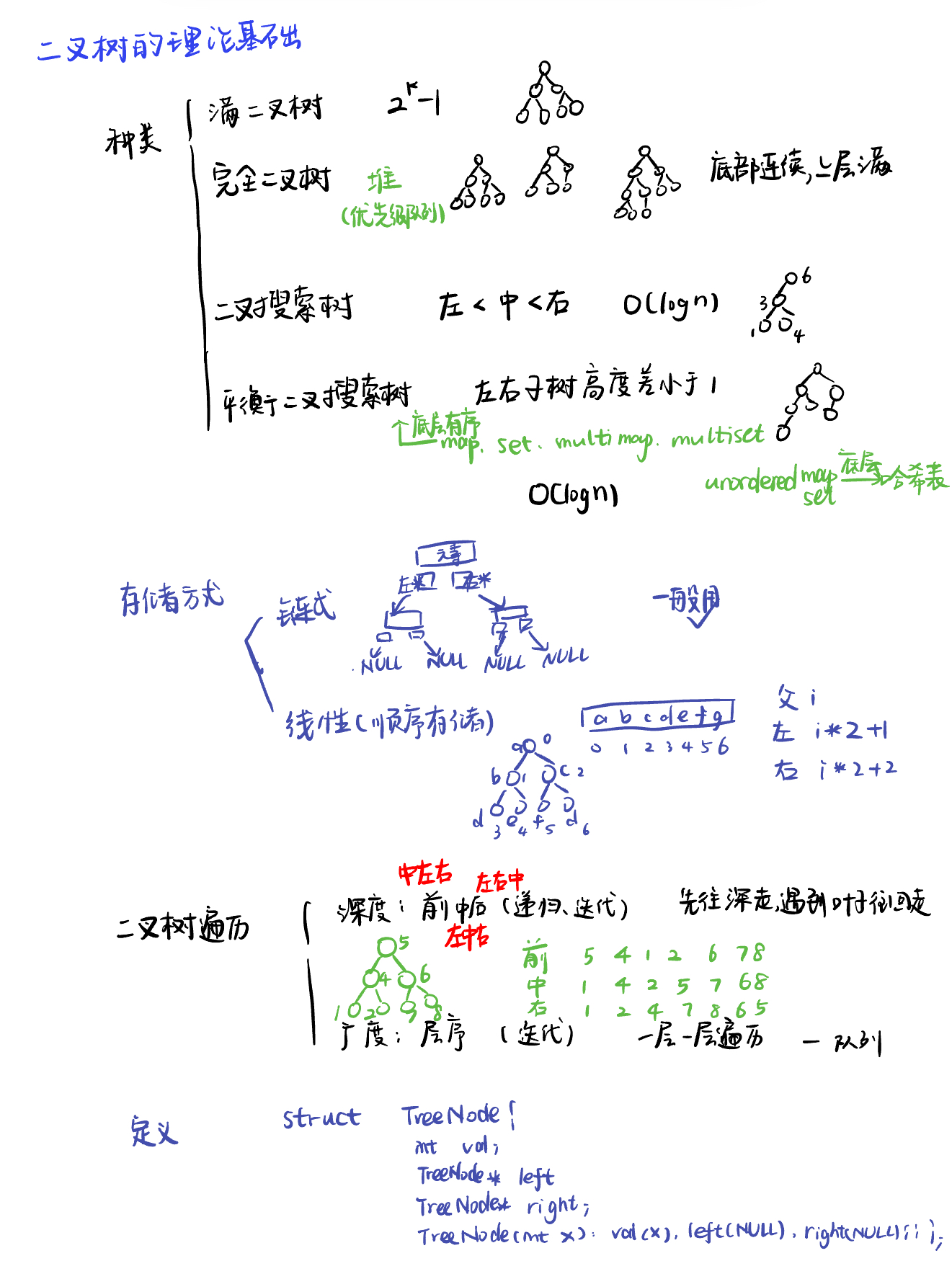
class TreeNode:
    def __init__(self, val, left = None, right = None):
        self.val = val
        self.left = left
        self.right = right

二叉树的递归遍历

Learning Materials

Leetcode前序

Leetcode中序

Leetcode后序

前序递归遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        def preorder(node):
            if node is None : 
                return
            res.append(node.val)
            preorder(node.left)
            preorder(node.right)
        preorder(root)
        return res

中序递归遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        def inorder(node):
            if node is None : 
                return
            inorder(node.left)
            res.append(node.val)
            inorder(node.right)
        inorder(root)
        return res

后序递归遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        def postorder(node):
            if node is None : 
                return
            postorder(node.left)
            postorder(node.right)
            res.append(node.val)
        postorder(root)
        return res

理论基础

Learning Materials

Leetcode前序

Leetcode中序

Leetcode后序

前序的遍历节点和处理节点的顺序一致，后序也类似，代码类似

根节点为空则返回空列表，时刻注意判空

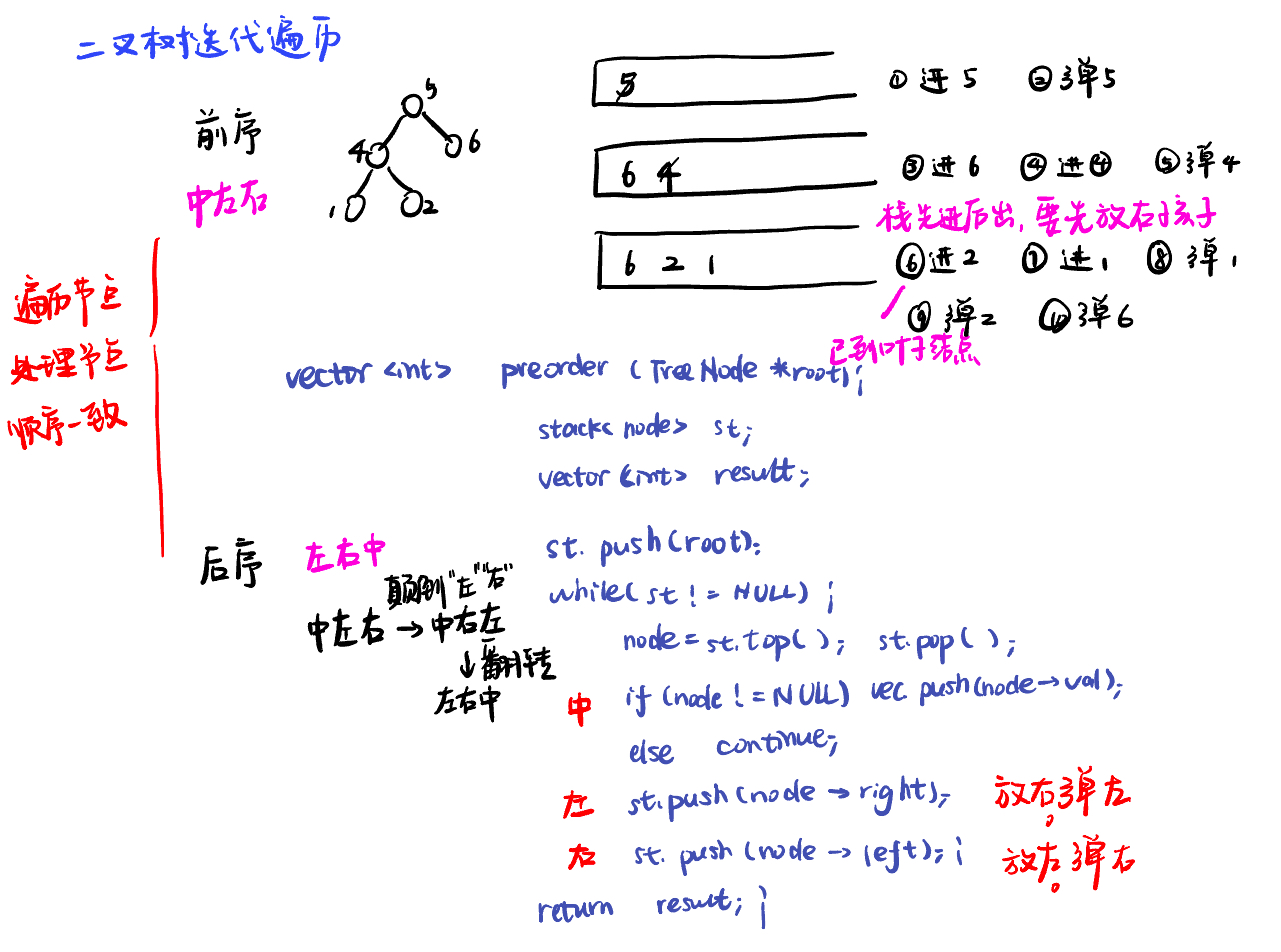
• 前序遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        st = []
        result = []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node:
                result.append(node.val)
            if node.right:
                st.append(node.right)
            if node.left:
                st.append(node.left)
        return result

• 后序遍历：一颠左右，二翻转

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        st = []
        result = []
        if root:
            st.append(root)
        while st:
            node = st.pop()
            if node:
                result.append(node.val)
            if node.left:  
                st.append(node.left)
            if node.right:
                st.append(node.right)
        return result[::-1]

中序遍历：

因为前序遍历中访问节点（遍历节点）和处理节点（将元素放进result数组中）可以同步处理，但是中序就无法做到同步。

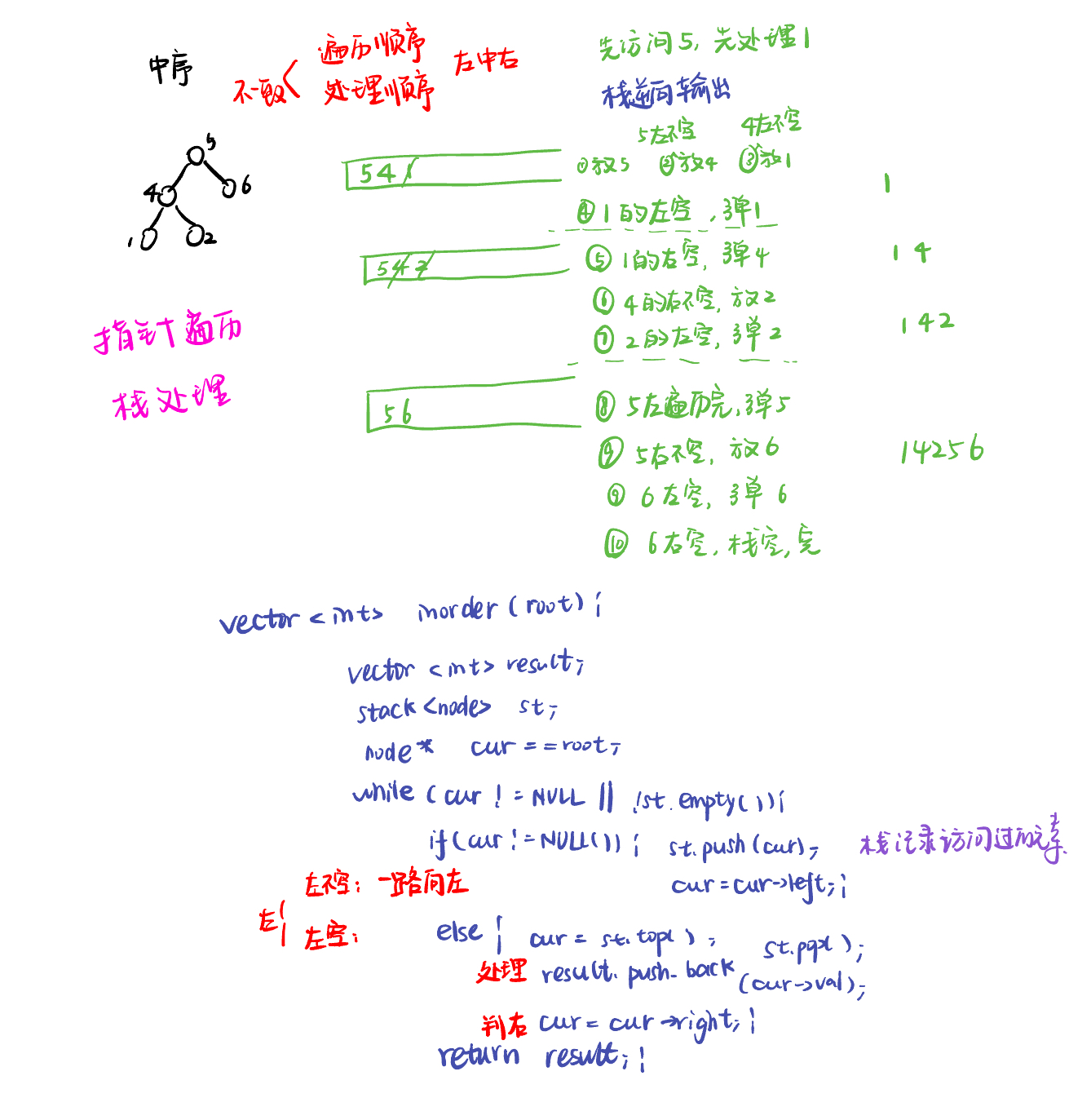
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        st = []
        result = []
        if not root:
            return []
        node = root
        while node or st:    # 如果是and的话，就没法运行else分支了。
            if node: # 先迭代访问最底层的左子树节点
                st.append(node)
                node = node.left 
            else: # 到达最左节点后处理栈顶节点
                node = st.pop()
                result.append(node.val)
                node = node.right
        return result

二叉树的统一迭代法：迭代但只改变两行顺序

Learning Materials

Leetcode前序

Leetcode中序

Leetcode后序

如何处理风格不统一的问题？先想问题是如何造成的。使用栈的话，无法同时解决访问节点（遍历节点）和处理节点（将元素放进结果集）不一致的情况。

因此，那我们就将访问的节点放入栈中，把要处理的节点也放入栈中但是要做标记。

如何标记呢？

方法一：就是要处理的节点放入栈之后，紧接着放入一个空指针作为标记。 这种方法可以叫做空指针标记法。

方法二：加一个 boolean 值跟随每个节点，false (默认值) 表示需要为该节点和它的左右儿子安排在栈中的位次，true 表示该节点的位次之前已经安排过了，可以收割节点了。 这种方法可以叫做boolean 标记法。

空指针标记法

由于栈先进后出，因此中序遍历是左中右，代码为右中左；前序遍历是中左右，代码为右左中；后序遍历的左右中，代码为中右左。

• 中序遍历：把中节点放入，不空的话：取出中，放入右、中（再次放入）、NULL、左；空的话：去栈的NULL、访问栈的top

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        st = []
        result = []
        if root:
            st.append(root)
        
        while st:
            node = st.pop() // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中（→if语句）   // 将空节点弹出 （→else语句）
            if node:
                if node.right:
                    st.append(node.right)  // 添加右节点（空节点不入栈）
                st.append(node)   // 添加中节点
                st.append(None)  // 中节点访问过，但是还没有处理，加入空节点做为标记。
                if node.left:
                    st.append(node.left)  // 添加左节点（空节点不入栈）
            else:   // 只有遇到空节点的时候，才将下一个节点放进结果集
                node = st.pop()  // 重新取出栈中元素
                result.append(node.val) // 加入到结果集
        
        return result

• 中序遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        st = []
        result = []
        if root:
            st.append(root)
        
        while st:
            node = st.pop()
            if node:
                st.append(node)
                st.append(None)
                if node.right:
                    st.append(node.right)
                if node.left:
                    st.append(node.left)
                
            else:
                node = st.pop()
                result.append(node.val)
        
        return result

• 前序遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        st = []
        result = []
        if root:
            st.append(root)
        
        while st:
            node = st.pop()
            if node:
                if node.right:
                    st.append(node.right)
                if node.left:
                    st.append(node.left)
                st.append(node)
                st.append(None)
            else:
                node = st.pop()
                result.append(node.val)
        
        return result

boolean 标记法

• 中序遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        result = []
        st = [(root, False)] if root else []

        while st:
            node, visited = st.pop()  # 多加一个 visited 参数
            if visited: # visited 为 True，表示该节点和两个儿子的位次之前已经安排过了，现在可以收割节点了
                result.append(node.val)
                continue
            # visited 当前为 False, 表示初次访问本节点，此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
            # 中序遍历是'左中右'，右儿子最先入栈，最后出栈。
            if node.right:
                st.append((node.right, False))
            st.append((node,True)) # 把自己加回到栈中，位置居中。同时，设置 visited 为 True，表示下次再访问本节点时，允许收割
            if node.left:
                st.append((node.left, False)) # 左儿子最后入栈，最先出栈
        
        return result

• 前序遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        result = []
        st = [(root, False)] if root else []

        while st:
            node, visited = st.pop()  # 多加一个 visited 参数
            if visited: # visited 为 True，表示该节点和两个儿子的位次之前已经安排过了，现在可以收割节点了
                result.append(node.val)
                continue
            # visited 当前为 False, 表示初次访问本节点，此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
            # 前序遍历是'中左右'
            if node.right:
                st.append((node.right, False))
            if node.left:
                st.append((node.left, False)) # 左儿子最后入栈，最先出栈
            st.append((node,True)) # 把自己加回到栈中，位置居中。同时，设置 visited 为 True，表示下次再访问本节点时，允许收割
            
        return result

• 后序遍历：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        result = []
        st = [(root, False)] if root else []

        while st:
            node, visited = st.pop()  # 多加一个 visited 参数
            if visited: # visited 为 True，表示该节点和两个儿子的位次之前已经安排过了，现在可以收割节点了
                result.append(node.val)
                continue
            # visited 当前为 False, 表示初次访问本节点，此次访问的目的是“把自己和两个儿子在栈中安排好位次”。
            # 后序遍历是'左右中'
            st.append((node,True)) # 把自己加回到栈中，位置居中。同时，设置 visited 为 True，表示下次再访问本节点时，允许收割
            if node.right:
                st.append((node.right, False))
            if node.left:
                st.append((node.left, False)) # 左儿子最后入栈，最先出栈
        
        return result

二叉树的层序遍历

Learning Materials

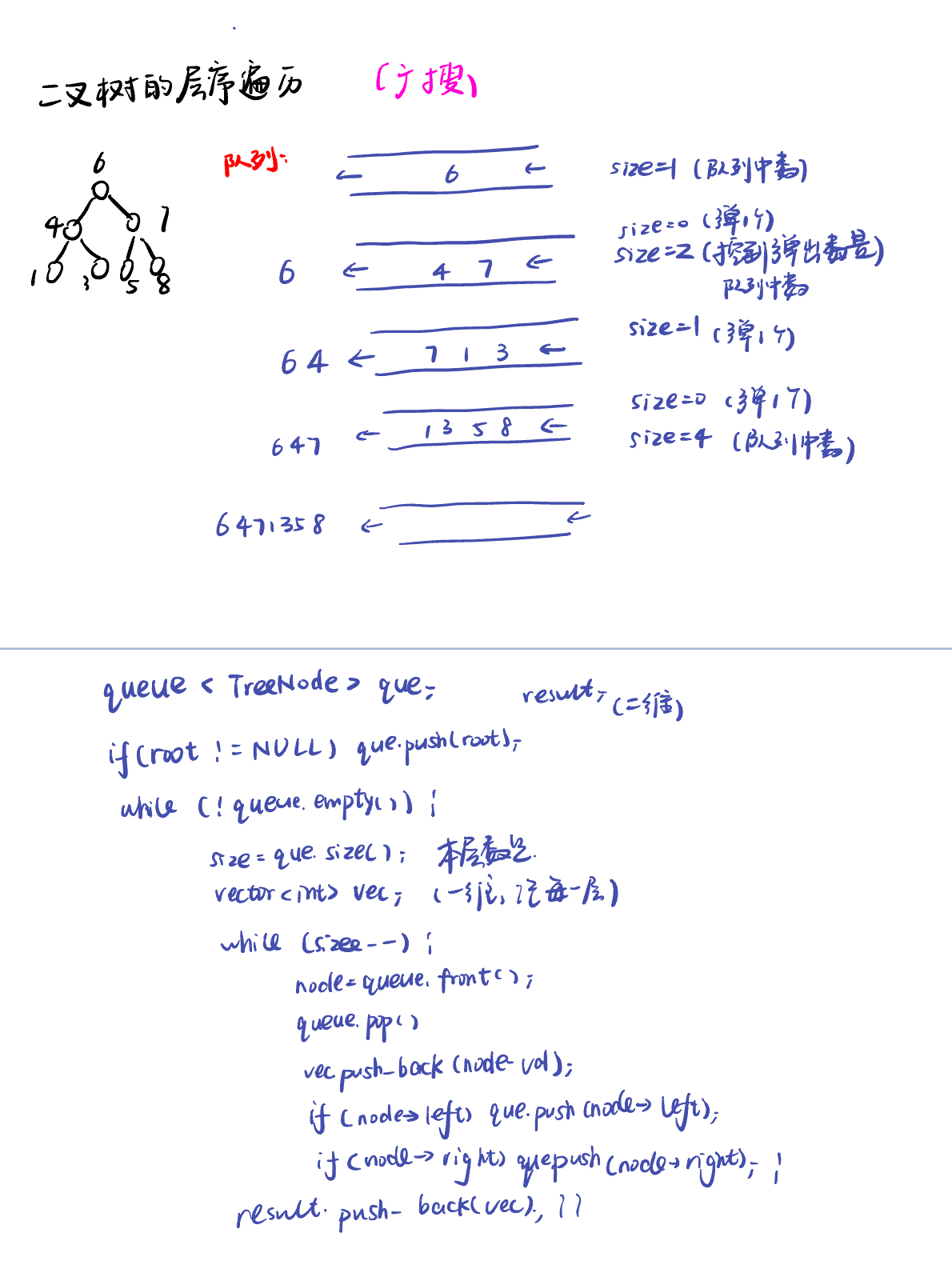
102.二叉树的层序遍历(opens new window)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        result = []
        que = deque([root])
        while que :
            size = len(que)
            vec = []
            while size:
                node = que.popleft()
                vec.append(node.val)
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
            result.append(vec)
        return result

• 递归版：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        levels = []

        def traverse(node, level):
            if not node:
                return
            if len(levels) == level:
                levels.append([])
            levels[level].append(node.val)
            traverse(node.left, level + 1)
            traverse(node.right, level + 1)
        traverse(root, 0)
        return levels

• 代码思路 这段代码使用了深度优先搜索（DFS）的递归方法来实现二叉树的层序遍历。具体思路如下：
  1. 边界条件检查：首先检查根节点是否为空，如果为空则直接返回空列表。
  2. 初始化结果列表：创建一个空列表 levels 用于存储每一层的节点值。
  3. 定义递归函数：定义一个内部递归函数 traverse，该函数接受两个参数：当前节点 node 和当前节点所在的层级 level。
  • 递归终止条件：如果当前节点为空，则直接返回。
  • 检查当前层级是否需要创建新列表：如果 levels 列表的长度等于当前层级 level，说明还没有为该层级创建列表，需要在 levels 中添加一个空列表。
  • 添加当前节点值到对应层级列表：将当前节点的值添加到 levels 中对应层级的列表中。
  • 递归遍历左右子树：分别递归调用 traverse 函数处理当前节点的左子节点和右子节点，同时将层级加 1。
    1. 启动递归：调用 traverse 函数，从根节点开始，层级为 0。
    2. 返回结果：返回存储每一层节点值的二维列表 levels。

107.二叉树的层次遍历II(opens new window)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def levelOrderBottom(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        result = []
        que = deque([root])
        while que :
            size = len(que)
            vec = []
            while size:
                node = que.popleft()
                vec.append(node.val)
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
            result.append(vec)
        return result[::-1]  #自底向上遍历

199.二叉树的右视图(opens new window)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def rightSideView(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        result = []
        que = deque([root])
        while que :
            size = len(que)
            for i in range(size):
                node = que.popleft()
                if i == size - 1:
                    result.append(node.val) # 将每一层的最后元素放入result数组中，只需要记录每层最右的数
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
        return result

637.二叉树的层平均值(opens new window)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def averageOfLevels(self, root: Optional[TreeNode]) -> List[float]:
        if not root:
            return []
        result = []
        que = deque([root])
        while que :
            size = len(que)
            levelsum = 0  #额外记录一下每层的和
            for i in range(size):
                node = que.popleft()
                levelsum += node.val
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
            result.append(levelsum / size)
        return result

429.N叉树的层序遍历(opens new window)

"""
# Definition for a Node.
class Node:
    def __init__(self, val: Optional[int] = None, children: Optional[List['Node']] = None):
        self.val = val
        self.children = children
"""

class Solution:
    def levelOrder(self, root: 'Node') -> List[List[int]]:
        if not root:
            return []
        result = []
        que = deque([root])
        while que :
            size = len(que)
            vec = []
            while size:
                node = que.popleft()
                vec.append(node.val)
                for child in node.children:
                    que.append(child)
                size -= 1
            result.append(vec)
        return result

515.在每个树行中找最大值(opens new window)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def largestValues(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        result = []
        que = deque([root])
        while que :
            size = len(que)
            vec = []
            while size:
                node = que.popleft()
                vec.append(node.val)
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
            result.append(max(vec))
        return result

116.填充每个节点的下一个右侧节点指针(opens new window)

本题依然是层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
        if not root:
            return root
        que = deque([root]) #创建一个 deque 对象 que，并将列表 [root] 中的元素依次添加到这个双端队列中。由于 [root] 只有一个元素 root，所以最终 que 这个双端队列中初始只有一个元素，即根节点 root。
        while que :
            size = len(que)
            prev = None
            while size:
                node = que.popleft()
                if prev:
                    prev.next = node
                prev = node
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
        return root

117.填充每个节点的下一个右侧节点指针II(opens new window)

这道题目说是二叉树，但116题目说是完整二叉树，其实没有任何差别，一样的代码一样的逻辑一样的味道。

"""
# Definition for a Node.
class Node:
    def __init__(self, val: int = 0, left: 'Node' = None, right: 'Node' = None, next: 'Node' = None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next
"""

class Solution:
    def connect(self, root: 'Node') -> 'Node':
        if not root:
            return root
        que = deque([root]) #创建一个 deque 对象 que，并将列表 [root] 中的元素依次添加到这个双端队列中。由于 [root] 只有一个元素 root，所以最终 que 这个双端队列中初始只有一个元素，即根节点 root。
        while que :
            size = len(que)
            prev = None
            while size:
                node = que.popleft()
                if prev:
                    prev.next = node
                prev = node
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
        return root

104.二叉树的最大深度(opens new window)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0 #返回深度
        result = []
        que = deque([root])
        while que :
            size = len(que)
            vec = []
            while size:
                node = que.popleft()
                vec.append(node.val)
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
            result.append(vec)
        return len(result) #返回深度

111.二叉树的最小深度

需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minDepth(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0
        que = deque([root])
        depth = 0 #额外记录一下深度
        while que :
            size = len(que)
            depth += 1
            while size:
                node = que.popleft()
                if node.left:
                    que.append(node.left)
                if node.right:
                    que.append(node.right)
                size -= 1
                if not node.left and not node.right:
                    return depth  #记录一下深度

This site is open source. Improve this page.